熱力学第一法則｜仕事と内部エネルギーの関係

熱力学第一法則とは，系における内部エネルギー $(U)$ ，気体が外部から吸収した熱量 $(Q)$ ，気体が外部にした仕事 $(W)$ の関係性を示す式です。

これらの関係性について，冒頭の式をもう一度確認してみましょう。

$$Q=\Delta{U}+W$$

系に加えられた熱（左辺）は，その一部が系が外部にする仕事に使われ，残りが系自体の内部エネルギー変化に使われる（右辺），と解釈することができます。

また，注意点として，「$W_{\text{した}}=-W_{\text{された}}$」　なので，第一法則を

$$Q+W=\Delta{U}$$

と表すこともあります。ここでの $W$ は $W_{\text{された}}$ を意味します。

こちらの式では，加えられた熱量と外部からされた仕事の和（左辺）が内部エネルギーの変化（右辺）になる，と解釈できますね。

内部エネルギーとはざっくりいうと温度のことですが，この式を活用する上ではこちらの理解が非常に重要となってきます。

怪しいなと感じた人は気体の内部エネルギーの意味と公式，求め方をチェックしてみてください。

内部エネルギーと仕事の関係の直感的な理解

まずは熱力学第一法則について， 図のように中に気体の入ったピストンを考えます。

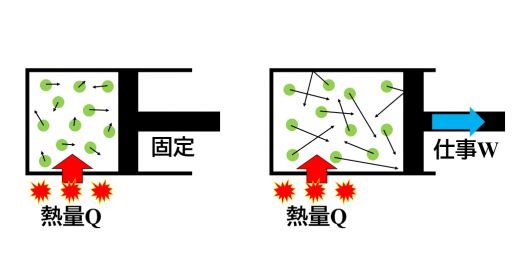
そこに熱 $(Q)$ を加えると，中の気体の温度が上がり，圧力も同時に上がります。

温度が上がると内部エネルギー $(U)$ が増加しますね。

同時に，圧力が上がることで外部に対してピストンは仕事 $(W)$ をします。

加えた熱量が外部に対する仕事と内部エネルギー変化につながる，ということです。

これが，熱力学第一法則

$$Q=\Delta{U}+W$$

の直感的な意味合いとなります。

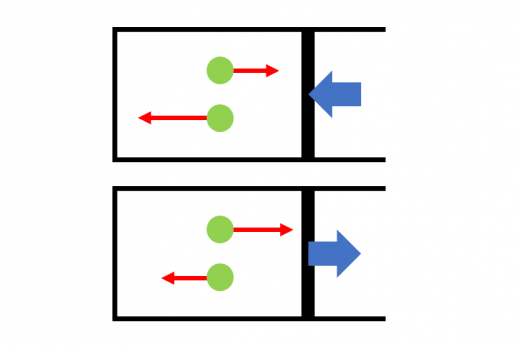
一方で，仕事と内部エネルギーの関係性として，

気体が圧縮される（外部から仕事をされる）とき，ピストンは内部に向かって動くため，

分子が壁に衝突した後の速さ > 衝突前の速さ

となります。

気体が膨張するときには，分子のスピードは衝突後の方が遅くなります。

（この説明は力積と運動量の関係を参照下さい。）

分子のスピード＝温度＝内部エネルギーとなるので，仕事と内部エネルギーの変化は上記のようになることが感覚的にわかりますね。

系が外部にする仕事は，系が外圧に抗して膨張することによります。

そのとき，仕事は

$$W=\int_{V_1}^{V_2}P_\text{外} \cdot dV$$

ただし，$P_\text{外}$ は外圧，$V_1$を元の体積，$V_2$を後の体積とします。

また，膨張するためには $P>P_\text{外}$ が必要です。

以下を参考に見てみましょう。

$（ex）$

$P$ が一定のとき，仕事は以下のように求められます。

$$\begin{aligned} W &= PS(x_2-x_1) \\ &= P(V_2-V_1) \end{aligned}$$

$P \times S(\text{面積})$ はかかる力，$(x_2-x_1)$ が距離を表しており，力学のときと仕事の表し方は変わらないことがわかりますね。

可逆変化での仕事

$P>P_\text{外}$でないと，膨張できません。

$$P+\varepsilon=P_\text{外}　(\varepsilon>0)$$

ここで $\varepsilon \to +0$ の極限では，系は事実上各瞬間で外部との釣り合いを保ちながら膨張しています。（ex.ピストン）

このような変化を，準静的変化（ゆっくりとした変化）といい，これは可逆変化です。

このとき，$P=P_\text{外}$ だから，仕事は

$$W=\int_{V_1}^{V_2}P \cdot dV$$

と表すことができます。

非可逆変化での仕事

ここからは，非可逆変化について見ていきましょう。

外部が真空の状態と，系の内部で反応が起きるなどして，急激に圧力が変わる場合の２つを見ていきます。

気体が真空へ拡散する場合，$P_\text{外}＝0$ ゆえ，$W=0$ です。

もう一つの系の内部が急に大きな圧力をもった場合，$\varepsilon \neq 0$ 極限$（P>P_\text{外}）$ のとき，

$$\begin{cases} \ \text{気体が外部にする仕事}　W_1=\int_{}^{}P_\text{外}\cdot dV\\ \ \text{気体がピストンを押す仕事}　W_2=\int_{}^{}P\cdot dV\\ \end{cases}$$

の差，つまり，$\int_{}^{}(P-P_\text{外})\cdot dV$ は巨視的な運動エネルギーに変わります。

そして最終的に内部エネルギーに変わる（系の温度が高くなる）ので，余分な仕事は，やはり系の外にする仕事にはなりません。