J.J.トムソンによる比電荷の測定と電子の発見

電子の比電荷は陰極線の正体をつかむために奮闘した過程で測定された物理量です。陰極線に関する当時の科学者の議論を交えながら, 電子の発見について簡単に解説していきます。

陰極線の正体は何か

19世紀後半, 当時の科学者の関心は陰極線にあり, 陰極線の正体を明らかにすることに必死でした。

→陰極線

科学者たちは陰極線の正体について主に2つの説を唱えていました。荷電粒子説と波動説です。

• 荷電粒子説：陰極線は負の電荷を持った粒子の流れ

• 波動説：陰極線はエーテル振動によるもの

波動説に関しては, ヘルツ(独, 1857-1894)が行った陰極線が静磁場の影響を受けなかったという実験結果がサポートしていたそうです。

現在, 陰極線の正体は電子であり荷電粒子説が正しかったと明らかになりました。荷電粒子説の提唱に大きく貢献したのがトムソンです。

トムソンが比電荷を発見したことで, 原子よりも小さい物質の存在が明らかになりました。

比電荷の分子と分母を入れ替えた $\dfrac{m}{q} \mathrm{[kg / C]}$ を質量電荷比といいます。

比電荷の定義

比電荷は以下のように定義されます。

トムソンは実験を通じて, 陰極線中の物質の比電荷 $\dfrac{e}{m}$ が一定の値であることを確認しました。

比電荷の測定と電子の発見

そこで「比電荷の電気量と水素イオンの電気量が同じである」という仮定を立てると, 比電荷の質量は水素イオンの2000分の1となることを見出しました。

原子よりも小さい物質の存在を明らかにしたのです。

トムソンは当時, 水素よりも小さい微粒子のことをコ―パスル(微粒子を指す言葉)と名付けました。この微粒子が, 今でいう電子です。

トムソンが比電荷の算出に成功したことで陰極線の正体は電子であると結論付けられました。トムソンはいかにして比電荷の測定に成功したのでしょうか。

陰極線の主な特徴

トムソンの実験へ移る前に陰極線の主な特徴をおさらいします。陰極線は陰極から陽極へ流れる物質であり, 直進性があります。

電場と磁場を印加すると, 下図のようなことが起きます。

1. 陰極線に対し, 垂直に電場をかけると陽極側に引き寄せられる ⇒ 陰極線中の物質はマイナスの性質を持つ

2. 陰極線に磁石を近づけると, 陰極線はフレミング左手の法則に従い, ローレンツ力を受ける

上図の場合,　ローレンツ力は下向きに働いています。ここから, 比電荷を測定したトムソンの実験について解説します。

1897年トムソンは従来のクルックス管よりもさらに真空度が高いガラス管を用いて, 実験を行いました。下図は装置を横から見た図です。

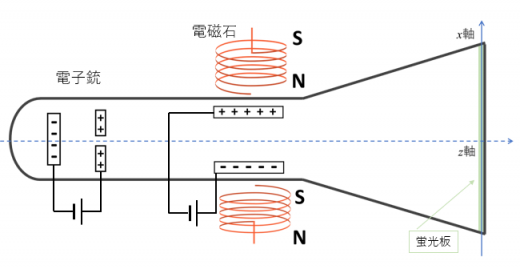
まず, 電子銃を使って陰極線を発生させます。陰極線の通り道には電極と電磁石が配置してあります。

陰極線中の電子は電極と電磁石の両方の影響を受けて曲がります。

トムソンがこの実験を行う頃, 真空ポンプの性能が向上したことで, 垂直電場の電位差がたった2Vでも陰極線が曲がるようになったそうです。

トムソンが真空度が高いガラス管を使用できたのは, エジソンが電球づくりのために開発した真空技術のおかげであったそうです。

陰極線は電場と磁場の2方向に曲がる

トムソンの実験を行うと, 電子はx軸とy軸の2つの方向に力を受けます。そして, 蛍光板上の座標 $P (\Delta x,\Delta y)$ に到達します。

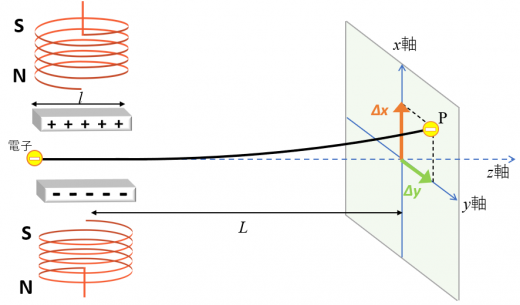
電子が到達した座標を $P$ として, 電子が電場と磁場から受ける力と運動を考えることで, 最終的に比電荷 $\dfrac{e}{m}$ を算出します。

電子が電場と磁場から受ける力をわけて考えていきます。

1. 電場の影響 → 電子は陽極側に引き付けられるため, x方向に曲げられる　⇒ xz平面(ガラス管を横から見た方向)で考える

2. 磁場の影響 → 電子はローレンツ力を受け, y方向に曲げれる ⇒ yz平面(ガラス管を上から見た方向)で考える

電場による電子の運動(x方向)

まず, 電場の影響を考え, xz平面(ガラス管を横から見た方向)で考えます。

この場合は電極中の領域①と, その後の蛍光板までの領域②におけるx方向とz方向の運動の違いを考える必要があります。

領域①において電子は電場の力を受け, x方向に等加速度運動をするのでそれを考慮する必要があります。

領域①：x方向の加速度運動

領域①に入る直前電子はz方向にのみ速度 $v_0$ を持っています。x方向の速度はありません。

領域①に物質Qが入ると, 電場から力を受けます。それを運動方程式($ma = F$)　で書き, 電子の加速度 $a\mathrm{ [m / s^2]}$ は以下のようになります。

$$\begin{aligned} ma &= eE \\ a &= \dfrac{eE}{m} \ \end{aligned}$$

電子の質量を$m$ [kg], 電子の電気量を $-e$ [C], 電場の強さを$E$ [V/m], x軸上向きを正としています。

z方向に力は作用しないため, z方向へは等速直線運動をします。(電場はx方向のみに作用するから)

そのため, z方向へは蛍光板にぶつかるまで初速 $v_0$ のまま進みます。領域①に電子がいる時間 $t_1$ は電極の長さ $l$ [m]を用いて,

$$t_1 = \dfrac{l}{v_0}$$

となり, 領域①中のx方向への変位は, x方向への加速度を用いて,

$$x_1 = \dfrac{1}{2} a t_1^2 = \dfrac{1}{2} \cdot \dfrac{eE}{m} \cdot \left(\dfrac{l}{v_0}\right)^2$$

となります。

→等加速度運動・等加速度直線運動の公式

領域②：慣性の法則による等速直線運動

領域①から領域②へ移る際の速度のx成分は,

$$v_x = at_1 =\dfrac{eE}{m} \cdot \dfrac{l}{v_0}$$

となります。領域②では電子に外力が働かないため, x方向とz方向どちらも等速直線運動になります(慣性の法則)。

慣性の法則〜ニュートンの第1法則〜

領域②の長さは $L- \dfrac{l}{2}$ であるため, 領域②を通過し蛍光板に到達するまでの時間 $t_2$ はz方向の速度 $v_0$ を用いて,

$$t_2 =\dfrac{L- \dfrac{l}{2}}{v_0}$$

となります。領域②におけるx方向への変位 $x_2$ は

$$x_2 = v_x t_2 = \dfrac{eE}{m}\cdot \dfrac{l}{v_0} \cdot \dfrac{ L- \dfrac{l}{2}}{v_0}$$

となります。よって領域①と領域②のx方向への変位を合計した$\Delta x$ は, 以下のように計算できます。

$$\begin{aligned} \Delta x &= x_1 + x_2 \\ &=\dfrac{1}{2} \cdot\dfrac{eE}{m} \cdot\left(\dfrac{l}{v_0}\right)^2 + \dfrac{eE}{m}\cdot \dfrac{l}{v_0}\cdot\dfrac{ L- \dfrac{l}{2}}{v_0} \\ & = \dfrac{eE}{m} {\left(\dfrac{1}{2}\cdot\left(\dfrac{l}{v_0}\right)^2 + \dfrac{l}{v_0}\cdot \dfrac{L- \dfrac{l}{2}}{v_0}\right)} \\ & = \dfrac{eE}{m} {\left(\dfrac{1}{2}\cdot \left(\dfrac{l}{v_0}\right)^2 + \dfrac{l}{v_0}\cdot\dfrac{L}{v_0} - \dfrac{1}{2} \cdot\left(\dfrac{l}{v_0}\right)^2\right)} \\ & = \dfrac{eE}{m} {\left( \dfrac{l}{v_0}\cdot\dfrac{L}{v_0}\right)} \\ & = \dfrac{eE}{m} {\left( \dfrac{lL}{v_0^2}\right)} \\ \end{aligned}$$

最後に, 左辺を比電荷 $\dfrac{e}{m}$ の形を目指して式変形すると, 以下のようになります。

$$\dfrac{e}{m} = \dfrac{v_0^2}{ElL} \cdot \Delta x$$

この式において, $v_0$ は未知数です。$v_0$ は電子が持つz方向への初速度です。この値を求めるために, 電子の磁場による影響を調べます。

磁場による電子の運動(y方向)

次に磁場が陰極線に与える影響について考えます。下図は実験装置を上から見た図です。

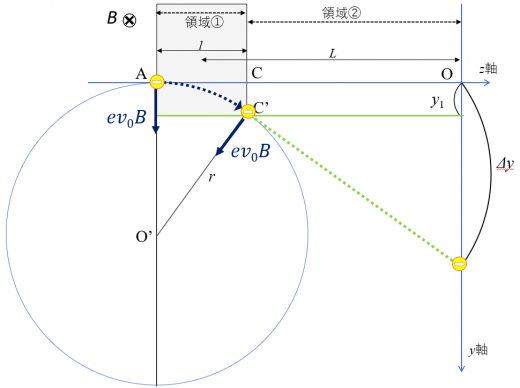
磁場は紙面手前から奥へ印加しています。磁場により電子はフレミングの左手の法則に従う向きにローレンツ力を受けます。すると, 領域①内では, 電子は円運動をします。

領域②では力が加わらないため, 等速直線運動をし蛍光面に到達します。地点C’から円軌道の接線方向に飛び出します。

領域①：ローレンツ力による円運動

領域①の円運動を考えます。磁束密度を $B$ [T]とすると, ローレンツ力の大きさは　$ev_0B$ [N] となります。円運動の運動方程式を考えると,

$$m\dfrac{v_0^2}{r} = ev_0B$$

となります。この式から円の半径 $r$ は次のように表すことができます。

$$\begin{aligned} m\dfrac{v_0}{r} &= eB \\ r &= \dfrac{mv_0}{eB} \end{aligned}$$

ここで, 図において$\triangle \mathrm{AA'C}$ (黄色の三角形)と$\triangle \mathrm{C'A'A''}$ (赤色の三角形)は相似より,

$$\mathrm{\dfrac{AA'}{AC'} = \dfrac{AC'}{A'A''}}$$

が成り立ちます。ここで, $\mathrm{A'A''}$($x_1$)は円の半径 $r$ に比べてとても小さいため($x_1 << r$),

$$\mathrm{A'A''}\simeq \mathrm{AA'} = 2r$$

という近似式が成り立ちます。(※物理ではこのような近似を頻繁に使います。)

図において, $\mathrm{AA'} = y_1$, $\mathrm{AC'} = l$ であり, 上記の相似の関係は以下のように書き直すことができます。

$$\dfrac{y_1}{l} = \dfrac{l}{2r}$$

$$r = \dfrac{l^2}{2y_1}$$

ここで円運動から求めた $r$ と相似から求めた $r$ を統合で結ぶと,

$$\begin{aligned} \dfrac{mv}{eB}&= \dfrac{l^2}{2y_1} \\ y_1 &= \dfrac{eBl^2}{2mv_0} \\ \end{aligned}$$

となり, $y_1$ を求めることができました。

領域②：慣性の法則による等速直線運動

ここから領域②について考え, $\Delta y$ を求めます。領域②では電子は等速直線運動をします。

図において$\triangle \mathrm{BC'C}$ (青色の三角形)と$\triangle \mathrm{BQO}$ (紫色の三角形)は相似より,

$$\mathrm{\dfrac{CC'}{BC} = \dfrac{OQ}{BO}}$$

の関係が成り立ちます。$\mathrm{CC'} = y_1$, $\mathrm{BO} = L$, $\mathrm{BC} = \dfrac{l}{2}$ で書き直すと,

$$\dfrac{y_1}{\frac{l}{2}} = \dfrac{\Delta y}{L}$$

が成り立ちます。よって, $\Delta y$ は

$$\Delta y = \dfrac{2L}{l} \cdot y_1$$

となります。

上で求めた$y_1$を代入すると, 以下のようになります。

$$\Delta y = \dfrac{2L}{l}\cdot \dfrac{eBl^2}{2mv_0} = \dfrac{eBlL}{mv_0}$$

左辺を比電荷 $\dfrac{e}{m}$ の形を目指して式変形すると, 以下のようになります。

$$\dfrac{e}{m} = \dfrac{v_0}{BlL} \cdot \Delta y$$

2式による比電荷の算出

電場による電子の運動(x方向)から以下の式が表れました。

$$\dfrac{e}{m} = \dfrac{v_0^2}{ElL} \cdot \Delta x$$

磁場による電子の運動から以下の式が表れました。

$$\dfrac{e}{m} = \dfrac{v_0}{BlL} \cdot \Delta y$$

これらの式を統合で結び, $v_0$を求めると,

$$\begin{aligned} \dfrac{v_0^2}{ElL} \cdot \Delta x &= \dfrac{v_0}{BlL} \cdot \Delta y\\ \dfrac{v_0}{E} \cdot \Delta x &= \dfrac{1}{B} \cdot \Delta y\\ v_0 &= \dfrac{E \cdot \Delta y}{B \cdot \Delta x } \end{aligned}$$

になります。この$v_0$ を $\dfrac{e}{m}$ の式に代入すれば比電荷を求めることができます。電場, 磁場どちらの式でも構いません。

• 電場の式ver.

$$\dfrac{e}{m} = \dfrac{v_0^2}{ElL} \cdot \Delta x = \dfrac{(\frac{E \cdot \Delta y}{B \cdot \Delta x})^2}{ElL} \cdot \Delta x = \dfrac{{E \cdot (\Delta y})^2}{B^2 l L \Delta x}$$

• 磁場の式ver.

$$\dfrac{e}{m} = \dfrac{v_0}{BlL} \cdot \Delta y = \dfrac{\frac{E \cdot \Delta y}{B \cdot \Delta x}}{BlL} \cdot \Delta y =\dfrac{{E \cdot (\Delta y})^2}{B^2 l L \Delta x}$$

右辺は電場 $E$, 磁場 $B$, 電極の幅 $l$, 電子の到達距離 $L$, 変位 $\Delta x, \Delta y$　は全て測定可能な量のため比電荷　$\dfrac{e}{m}$　を求めることが可能です。

上記の後半部分の磁場による電子の運動から初速度 $v_0$を求める方法以外にも, $v_0$ を求める方法あります。それを2つ紹介します。

電場と磁場で真っすぐ電子を飛ばす

一つ目の方法は電場と磁場による力を釣り合わせる方法です。

領域①において, 図のように電極と電磁石を配置します。この図では電磁石を棒磁石で表現しています。

電場と磁場の大きさを調整すると, 電場による力と磁場によるローレンツ力がつりあうときに真っすぐ電子を飛ばすことができます。

このとき, 以下のようなつり合いの式から $v_0$ が算出できます。

$$\begin{aligned} eE' &= ev_0B' \\ E' &= v_0B'\\ v_0 &= \dfrac{E'}{B'} \end{aligned}$$

電子が真っすぐ飛ぶように電場と磁場を調整できれば, 比較的に簡単な式で $v_0$ を求めることができます。

電子銃のエネルギーから $v_0$ を算出

2つ目の方法は電子銃のエネルギーから算出する方法です。

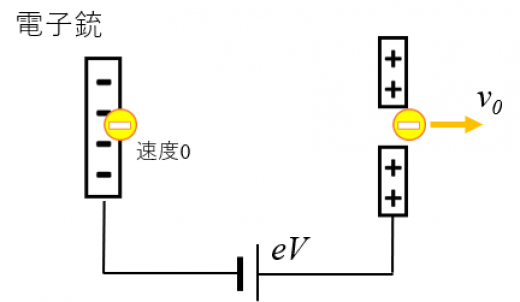
電子銃の電極間の電位差を$V$ [V]とすると極板間の位置エネルギーの差は $eV$ となります。電子の陰極における速度は $0$ [m/s]で, 陽極の速度は $v_0$ [m/s]です。

エネルギー保存則の式をたてると, $v_0$ は以下のように計算できます。

$$\begin{aligned} \dfrac{1}{2}m v_0^2 - \dfrac{1}{2}m 0^2 &= eV\\ \dfrac{1}{2}m v_0^2 &= eV\\ \dfrac{1}{2} v_0^2 &= \dfrac{e}{m}V\\ \dfrac{e}{m} &= \dfrac{v_0^2}{2V}\\ \end{aligned}$$

このエネルギー保存則だけでは, $v_0$ がわかりませんが, 電場ver.の式 $\dfrac{e}{m} = \dfrac{v_0}{BlL} \cdot \Delta y$ を用いると,

$$\begin{aligned} \dfrac{v_0^2}{2V} &= \dfrac{v}{BlL} \Delta y\\ \dfrac{v_0}{2V} &= \dfrac{1}{BlL} \Delta y \\ v_0 &= \dfrac{2V}{BlL} \Delta y\\ \end{aligned}$$

となり, $v_0$を求めることができます。また, 電位差$V$は電場$E''$と電荷$e$を用いて, $V=eE''$ と書けるので $v_0$を

$$v_0 = \dfrac{2eE''}{BlL}x \\$$

と書き直すことができます。