熱力学第二法則｜トムソン・クラウジウスの原理からカルノーの定理

トムソンの原理（これを「ケルビンの原理」と呼ぶこともあります。トムソンとケルビンは別人というわけではなく，単に同じ人物の異なる呼び方です。）と，クラウジウスの原理は実は同値であることを示すことができます。以下でこれを証明してみようと思います。

トムソンの原理→クラウジウスの原理

対偶「クラウジウスの原理を否定するような熱サイクルが存在している時，トムソンの原理を否定した熱サイクルが存在する」ことを示すことにします。

クラウジウスの原理を否定する熱サイクル $A$ を考えます。この熱サイクルは，低温熱浴から高温熱浴に熱を移すことができます。

$A$ とカルノーサイクル $C$ を動かすことを考えます。カルノーサイクルは高温熱浴から $Q_{\text{in}}$ を受け取り，低温熱浴から $Q_{\text{out}}$ を受け取って，$W = Q_{\text{in}} - Q_{\text{out}}$ の仕事をします。ここで，$A$ によって，$Q_{\text{out}}$ の熱を低温側から高温側に移します。

このとき，$A$ と $C$ を合わせた熱サイクルは，$Q_{\text{in}} - Q_{\text{out}}$ を受け取って，$Q_{\text{in}} - Q_{\text{out}}$ という仕事をする熱サイクルになります。この熱サイクルは，トムソンの原理に反するものになっています。

クラウジウスの原理→トムソンの原理

対偶「トムソンの原理を否定するような熱サイクルが存在している時，クラウジウスの原理を否定した熱サイクルが存在する」ことを示すことにします。

トムソンの原理を否定する熱サイクル $B$ を考えます。この熱サイクルは，受け取った熱を全て仕事に変えることのできる熱サイクルです。

$B$ と逆カルノーサイクル $C'$ を動かすことを考えます。$B$ は高温熱浴から $Q_{\text{in}}$ を受け取り，$Q_{\text{in}}$ の仕事をします。この仕事を $C'$ に与えることよって，$Q'_{\text{in}}$ の熱を低温側から吸収し，$Q'_{\text{out}} = Q'_{\text{in}} + Q_{\text{in}}$ の熱を高温側に移します。

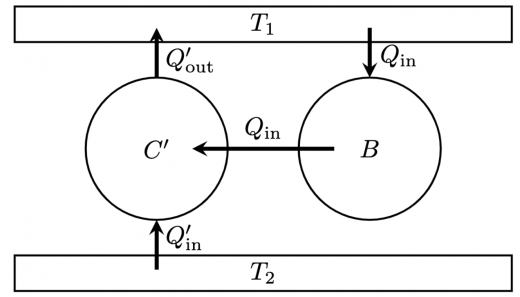
このとき，$B$ と $C'$ を合わせた熱サイクルは，$Q'_{\text{in}}$ の熱を外部に仕事を残さずに，低温側から高温側に移す熱サイクルになります。この熱サイクルは，クラウジウスの原理に反するものになっています。

以上で，トムソンの原理とクラウジウスの原理が等しいことが示されました。

ただ1つの熱源から熱を吸収し，ずっと動き続ける熱サイクルである，第二種永久機関があれば，世界にはびこる熱を吸収して仕事をすることができるので，エネルギー問題が瞬時に解決します。例えば，車を走らせる際，近くの空気の持つ熱を使って仕事をし，冷たくなった空気を吐き出して，永遠に走る車があったら，どんなに素晴らしいことでしょう。

しかし，長年の研究の末，残念ながらそんなものはどうやらないらしい，ということがわかりました。これを原理として取り上げたものが，オストヴァルトの原理です。

トムソンの原理は，オストヴァルトの原理と同値な言い換えであることは，定義から明らかです。第二種永久機関は，トムソンの原理で存在が否定されている熱サイクルそのものだからです。

トムソンの原理とクラウジウスの原理は同値なので，もちろんオストヴァルトの原理とクラウジウスの原理も同値です。

ここまでで，「トムソンの原理」「クラウジウスの原理」「オストヴァルトの原理」が全て等しい主張であることをみておきました。これらのうち，自分が一番当たり前だと思うものを原理として認めてください。それが熱力学第二法則です。例えば，あなたが，トムソンの原理を認めたとすれば，定理としてクラウジウスの原理とオストヴァルトの原理が成り立つことが証明できます。

熱力学第二法則から，次のカルノーの定理を導くことができます：

任意の可逆熱機関の熱効率は理想気体のカルノーサイクルの熱効率に等しい

まずは定理の前半部分から証明していきます。

任意の可逆サイクル $D$ の逆サイクル $D'$ と，理想気体のカルノーサイクル $C$ を同時に動かすことを考えます。熱と仕事の受け渡しは，上図のように行われるとします。このとき，クラウジウスの原理から， $$Q_{C1} \geq Q_{D'1}$$ が成立している必要があります。

また，$C,D'$ は可逆なサイクルであるから，真逆にサイクル動かせば，同様に $$Q_{C1} \leq Q_{D'1}$$ であることが示せます。よって， $$Q_{C1} = Q_{D'1}$$ が成立します。この式と熱力学第一法則から， $$Q_{C2} = Q_{D'2}$$ が成立することもすぐにわかります。これより， $$\begin{aligned} \eta' &= 1 - \dfrac{Q_{D'1}}{Q_{D'2}}\\ &= 1 - \dfrac{Q_{C1}}{Q_{C2}}\\ &= \eta \end{aligned}$$ と計算できるので，主張は示されました。

不可逆な熱機関の熱効率は理想気体のカルノーサイクルの熱効率より小さい

次に定理の後半部分を示します。

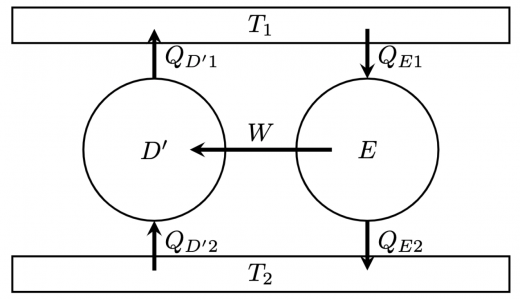
任意の可逆サイクル $D$ の逆サイクル $D'$ と，不可逆サイクル $E$ を考えます。クラウジウスの原理より， $$Q_{D'1} \leq Q_{E1}$$

ここで，$W = Q_{E1} - Q_{E2} = Q_{D'1} - Q_{D'2}$ であることを考慮すると， $$\begin{aligned} \eta'' &= 1 - \dfrac{Q_{E2}}{Q_{E1}} = \dfrac{Q_{E1} - Q_{E2}}{Q_{E1}}\\ &= \dfrac{Q_{D'1} - Q_{D'2}}{Q_{E1}}\\ &\leq \dfrac{Q_{D'1} - Q_{D'2}}{Q_{D'1}} = \eta' = \eta \end{aligned}$$ と計算できるので，主張は示されました。

任意のサイクルの熱効率が $\eta$ を超えないことがわかったので，$\eta$ が熱機関の理論的最大値ということになります。

今後の熱力学の理論の行く末をざっくり説明します。

上記のカルノーの定理を導出したのと同様にして，熱源が複数になったときのサイクルを考えると，クラウジウスの不等式と呼ばれる不等式を導出することができます。このカルノーの定理の結果は（特殊なケースでの）クラウジウスの不等式と呼ばれる式と同値になっています。

クラウジウスの不等式から，エントロピーと呼ばれる状態量を定義します。エントロピーを定義できると，さらに熱力学での考察対象が広がっていきます。エントロピーは統計力学と呼ばれる分野でも登場する，とても重要な概念です。

また，断熱過程の状態変化を考えると，不可逆な変化に対して，エントロピーは必ず増大します（可逆変化に対してはエントロピーは不変です）。これが有名な「エントロピー増大の原理」です。宇宙を系として考えるとすれば，断熱であることが保証されているはずです。もし断熱でないとすれば，宇宙の外にも何かしらの世界があることになってしまうからです。不可逆変化が必然的に起こりうるのが宇宙ですから，宇宙全体でみれば，エントロピーが増大する方向に進んでいると考えられています。