気体の状態変化とモル比熱(断熱変化,等温変化,定圧変化など)
気体の状態変化とは,気体の系において圧力,体積,温度が変化することを表します。
特に高校物理においては,熱力学第一法則とボイル・シャルルの法則を利用して,気体の状態がどのように変わるかを考察します。
なお,気体が外部から吸収した熱量を,による内部エネルギー変化を,気体が外部にした仕事をとして,
- 熱力学第一法則
- ボイル・シャルルの法則
と表します。
今回は圧力,体積,温度などの変数を固定し,気体の状態がどう変わるかをそれぞれの事例について説明していきます。
この記事に関連するQ&A
代表的な変化過程の状態図
代表的な変化過程の状態図
の理想気体の平衡状態は で表すことができます。
のうち,2つがわかれば残り1つも定まるので, ,, の3つの関係を調べれば十分です。
- 図(最もよく使われる)
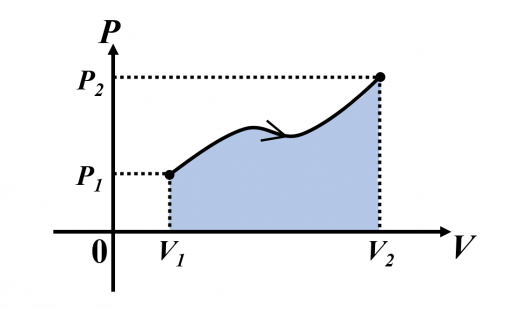
(ゆっくりとした変化なら,)
は斜線面積と一致します。
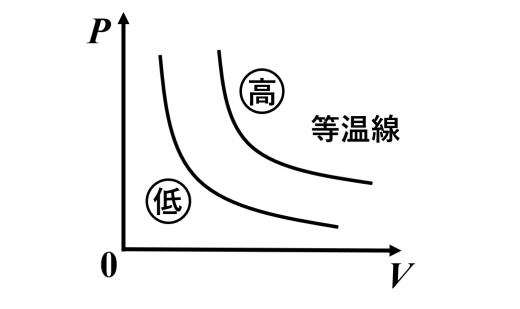
- 図
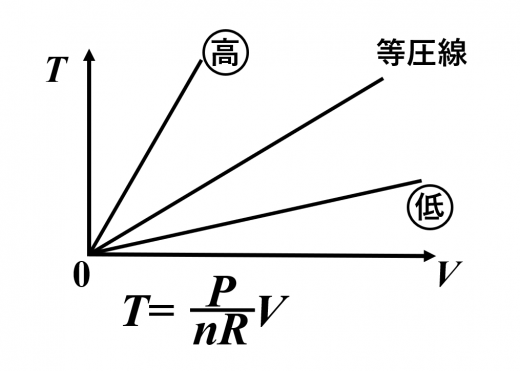
- 図
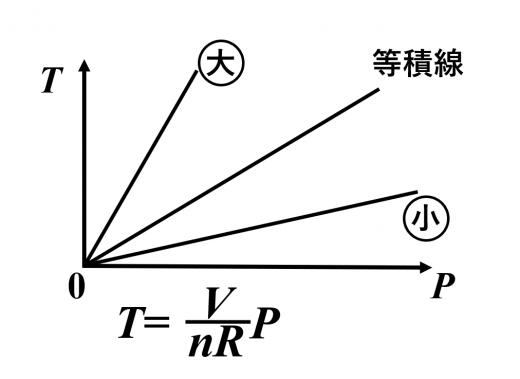
図がよく使われる2つの理由としては,
(ⅰ) 仕事 が視覚的に捉えられる
(ⅱ) の関係も見やすい
ということがあげられます。
モル比熱とは
モル比熱とは
モル比熱とは, の物質を 上昇させるのに必要な熱量のことです。
以下のように定義されます。
一見気体の状態変化とはあまり関係がないように思うかもしれませんが,この単元の理解には欠かせません。
固体,液体は,温度によりその体積が一義的に決まり,比熱もほとんど一義的に決まります。
一方で気体は,自由度が大きく,様々な経路で等しい温度変化が実現します。
つまり,変化に応じてそれぞれの比熱が定義されるということです。
定積変化
定積変化
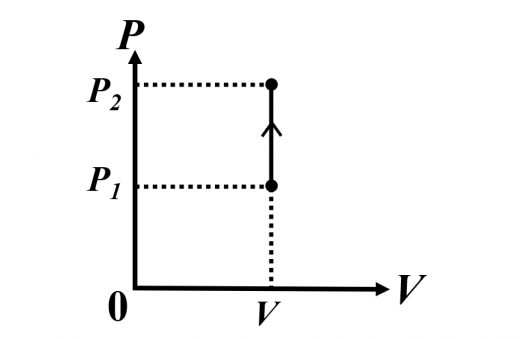
このとき,体積変化がないので, です。
熱力学第一法則より, となりますね。
また,
の が一定になるので,
つまり,圧力と温度が比例することがわかります。
定積モル比熱
ここで,定積変化のモル比熱 を考えます。
であり,
から,
特に,単原子分子理想気体では なので
常温の二原子分子理想気体では なので
となります。
内部エネルギーを と表す理由については,気体の内部エネルギーの意味と公式,求め方をご参照ください。
定圧変化
定圧変化
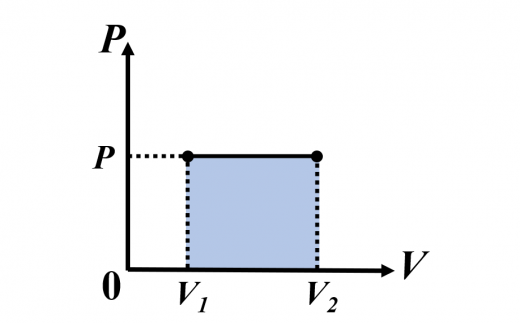
このとき, は斜線面積と等しいので
系が外部にする仕事は,系が外圧に抗して膨張することによります。
そのとき,仕事は
また,
の が一定になるので,
つまり,体積と温度が比例することがわかります。
定圧モル比熱
定圧変化でのモル比熱 を考えます。
単原子分子理想気体においては,
定圧変化において, は一定なので
が成り立ちますね。
②に③,④を代入して
定圧モル比熱 であることがわかりました。
マイヤーの関係式
マイヤーの関係式について説明します。
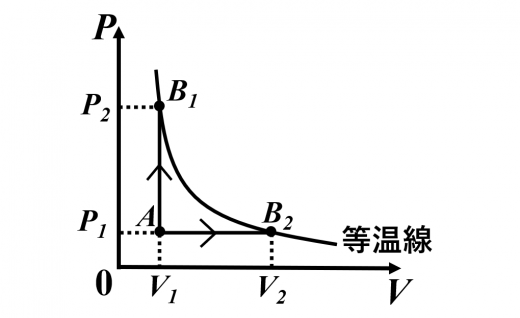
状態 (定積変化)と
状態 (定圧変化)は
違う経路ですが, がともに等しいので も等しくなります。
ここで,定積,定圧モル比熱の見出しの
から,
これをマイヤーの関係式といい,理想気体において成立します。
等温変化
等温変化

このとき,仕事 は
等温変化において, だから
熱力学第一法則より,
等温変化においては,
となりますね。
断熱変化
断熱変化
断熱変化では,熱の移動が行われないので,
熱力学第一法則より,
つまり,直感的な理解としては,
となります。
さて,気体の系を断熱的 に”ゆっくり”と変化させることを考えてみます。
微小変化 をみてみましょう。
から,熱力学第一法則より,
で両辺を割ると,
つまり, が成立することがわかりますね。
を代入して整理すると,
が成り立ちます。
ここで,比熱比 を定義します。
すると,断熱変化では
が成立します。
これらを,断熱変化に関するポアソンの式といいます。
気体の状態変化においては,どの変数が固定されているのかと,変数同士の関係を正しく理解することが鍵です。








