電場・磁場・電荷密度・電流密度｜電磁気学における基本的な物理量

更新 2021/05/29

電磁気学において登場する物理的な対象は限られています。この記事では，電場，磁場，電荷密度，電流密度について，どのように定義がなされるのかをみていきます。これらの定義をしっかり理解した上で，電磁気学の理論展開を追っていきましょう。

電場の定義

電荷 $q$ の荷電粒子を位置 $\boldsymbol{x}$ に静止しておいたときに $\boldsymbol{F}(\boldsymbol{x},t)$ の力が電荷に加わるとすると， $\boldsymbol{E}(\boldsymbol{x},t) :=\frac{\boldsymbol{F}(\boldsymbol {x},t)}{q}$ によって定義されるベクトル場 $\boldsymbol{E}(\boldsymbol{x},t)$ を電場といいます。

磁場の定義

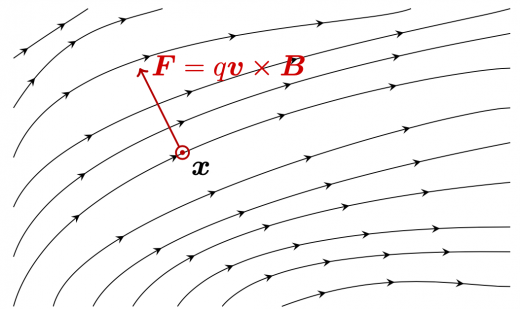
また，電場のない $\boldsymbol{E}(\boldsymbol{x},t)=0$ の場合でも，電荷を動かすと力が働くことがあります。この力を与えるベクトル場 $\boldsymbol{B}(\boldsymbol{x},t)$ を磁場といいます。位置 $\boldsymbol{x}$ にある電荷 $q$ の荷電粒子が速度 $\boldsymbol{v}$ で動いているとき，磁場 $\boldsymbol{B}(\boldsymbol{x},t)$ によって荷電粒子に働く力 $\boldsymbol{F}(\boldsymbol{x},t)$ は $\boldsymbol{F}(\boldsymbol{x},t) =q\boldsymbol{v}\times\boldsymbol{B}(\boldsymbol{x},t)$ となります（下図は紙面手前方向に正電荷が向かってきているとき）。

この漢字の読みを教えてください 2

有理化をしないでtに置き換えて計算すると答えが違くなってしまうんですが何故ですか？どこか間違ってますか？ 3

シリンジに栓をして引っ張り、栓を外した時の吸引力はそのシリンジの体積で強くなりますか？それを示す数式などはありますか？ 4

数三でロピタルの定理なみに使う定理を教えてください 5

ローレンツ力

電場 $\boldsymbol{E}(\boldsymbol{x},t)$ も磁場 $\boldsymbol{B}(\boldsymbol{x},t)$ も存在しているとき，荷電粒子に働く力をまとめると $\boldsymbol{F}(\boldsymbol{x},t) =q\boldsymbol{E}(\boldsymbol{x},t)+q\boldsymbol{v}\times\boldsymbol{B}(\boldsymbol{x},t)$ となります。この力を Lorentz（ローレンツ）力といいます。

これは，電場や磁場という物理的な対象が，電荷という物理的な対象に与える力を数式で表したものです。電場と磁場が分かれば，粒子に働く力がわかるので，そのあとの挙動を予想するのは力学の問題になります。

電荷密度

単位体積あたりの電荷を電荷密度 ρ\rhoρ といいます。電荷はスカラーなので電荷密度もスカラーです。電荷密度は空間上の各点で異なるときには ρ(x)\rho(\boldsymbol{x})ρ(x) と書きます。さらに時間の経過とともに電荷密度が変化する場合には ρ(x,t)\rho(\boldsymbol{x},t)ρ(x,t) と書きます。
領域 V\text{V}V で電荷密度 ρ(x,t)\rho(\boldsymbol{x},t)ρ(x,t) が与えられているとき，領域 V\text{V}V の電荷 Q(t)Q(t)Q(t) は ρ(x,t)\rho(\boldsymbol{x},t)ρ(x,t) の足しあわせで，
    Q(t)=∫Vρ(x,t) dV
    Q(t)
    =\int_\text{V}\rho(\boldsymbol{x},t)\, d{V}
    Q(t)=∫V​ρ(x,t)dV
となります（左辺は領域 V\text{V}V における体積積分を表しています）。

電流密度

電流とは単位時間あたりに（導線の）断面を通過する電荷量を表していました。すなわち，電流 $I$ が時間経過によって変化しない定常流であれば，時間 $\varDelta t$ の間に導線の断面を流れる電荷 $\varDelta Q$ は $\varDelta Q =I\varDelta t$ と表されます。時間によって変化する電流 $I(t)$ を考えるときには， $\varDelta Q =\int_{\varDelta t}I(t)\, dt$ となります。

では，導線ではなく，もっと一般的な空間を電荷が流れているときにはどうすれば良いでしょうか。導線の場合には断面が固定されていました（導線に垂直な方向に電荷が流れることは考えませんよね）が，一般の空間を考える際には断面を自由にとってその断面を通過する電流が知りたいと思うでしょう。そこで登場するのが電流密度です。

単位面積あたりに通過する電流を電流密度 $\boldsymbol{j}$ といいます。電流密度はベクトルで，ベクトルの向きは電荷の流れている方向を表します。電荷密度と同様に，空間依存や時間依存の電流密度を考えるときには $\boldsymbol{j}(\boldsymbol{x},t)$ などと書きます。

ある断面 $\text{S}$ を指定すればその断面を通過する電流 $I(t)$ を計算することができて， $I(t) =\int_\text{S}\boldsymbol{j}(\boldsymbol{x},t)\cdot d{\boldsymbol{S}} =\int_\text{S}\boldsymbol{j}(\boldsymbol{x},t)\cdot\boldsymbol{n}\, d{S}$ となります。 $\boldsymbol{n}$ は断面 $\text{S}$ に垂直な法線ベクトルです。法線ベクトルは表と裏で２つ取れますが，法線ベクトルの方向に電流の正の向きを取るということになります。また，慣例として $\boldsymbol{n}\, dS=: d\boldsymbol{S}$ としてしまうこともあります。

電流密度

上図を見ると電流 $I$ がベクトルだと思うかもしれませんが，電流 $I$ はスカラーであることに注意しましょう。断面とそれに対応する法線ベクトルを指定すれば，電流の向きは指定されてしまうので，情報としてはスカラー量だけで十分です。

ここでは電流から電流密度を定義しましたが，電荷密度 $\rho(\boldsymbol{x},t)$ と電荷の速度 $\boldsymbol{v}(\boldsymbol{x},t)$ を用いて $\boldsymbol{j}(\boldsymbol{x},t) :=\rho(\boldsymbol{x},t)\boldsymbol{v}(\boldsymbol{x},t)$ と定義することもできます。実際にこの定義で与えられる電流密度 $\boldsymbol{j}$ も断面積で積分すれば電流 $I$ が出てくるということを確認してみましょう。

電流密度2

証明

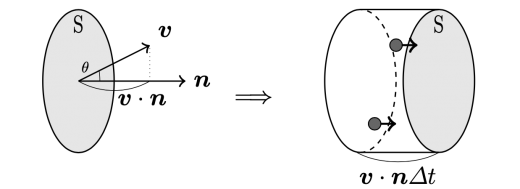
$\boldsymbol{j}:=\rho\boldsymbol{v}$ で定義される電流密度が電流を与えることを示す。微小面積 $\varDelta S$ の断面 $\text{S}$ とその法線ベクトル $\boldsymbol{n}$ を考える。時間 $\varDelta t$ の間に電荷が断面 $\text{S}$ を垂直に通過する長さは，法線ベクトル $\boldsymbol{n}$ と速度 $\boldsymbol{v}$ のなす角 $\theta$ を用いて $v\cos\theta\varDelta t=\boldsymbol{v}\cdot\boldsymbol{n}\varDelta t$ と表される。したがってこの断面を垂直に通過する電荷は体積 $\boldsymbol{v}\cdot\boldsymbol{n}\varDelta t\varDelta S$ の立体内に含まれる電荷を計算すれば良い。体積 $\boldsymbol{v}\cdot\boldsymbol{n}\varDelta t\varDelta S$ に電荷密度 $\rho$ をかけて， $\begin{aligned} \varDelta Q &=\rho\boldsymbol{v}\cdot\boldsymbol{n}\varDelta t\varDelta S\\ &=\boldsymbol{j}\cdot\boldsymbol{n}\varDelta S\varDelta t. \end{aligned}$ これが $\varDelta Q=\varDelta I\varDelta t$ に等しいので， $\varDelta I =\boldsymbol{j}\cdot\boldsymbol{n}\varDelta S$ を得る。もっと面積の大きな断面 $\text{S}$ を考えるときにはこれを面積分すればよく， $I =\int_\text{S}\boldsymbol{j}\cdot\boldsymbol{n}\, dS$ となる。 $\blacksquare$

電磁気学の登場人物は限られています。