光電効果と仕事関数を箔検電器の実験から理解する

更新 2021/06/17

今回は, 光が単純な波ではなく, 粒子(ツブツブ)であることを証明した光電効果について解説します。
光電効果が観測される前, 光は波であると考えられていました。しかし, 光電効果という現象が観測されたことで, 光の粒子性が明らかとなりました。
光電効果の観測によって, 光量子仮説(光は波と粒子の二面性を持つこと)がささやかれるようになりました。
本記事では,
光電効果という現象
光電効果が確認された実験内容
光が単なる波ではなくの粒子でもあると結論付けられた背景
について詳しく解説していきます。

光の波動説から光量子仮説へ

1807年にトーマス・ヤングが行った「光の干渉」の実験により, 光が二重スリットの先で干渉縞が確認されたことから, 「光は波である」という光の波動説が当時の科学者の中で主流となりました。
もし, 光が単純な粒子ならば干渉は起きないためです。
→ヤングの干渉実験
光は波でも粒子であるという「光量子仮説」しかし, 1887年にハイレンヒッツ・ヘルツにより光電効果という現象が確認されたことで, 光は粒子(ツブツブ)である「光の粒子説」が浮上しました。
後にアインシュタインやミリカンによって, この粒子説が裏付けられました。二人はこの研究に関してノーベル物理学賞を獲得しています。
アインシュタインは光は波と粒子の両方の性質も持つ物質であるという「光量子仮説」によりノーベル物理学賞を受賞しました。
ミリカンは光電効果と電気素量に関する研究でノーベル物理学賞を受賞しています。
次に, 光電効果とはどんな現象かを解説します。

エッセンス熱力学の問題です 2枚目の解き方がダメな理由が分かりません、誰か教えて頂けませんか……？正しい答えは58/9 2

消費される電力の合計がいくらかという問題です。電球に使われるフィラメントのように，電流によって温度が大きく変化する導 3

エッセンスから熱力学の問題です。この問題の解き方が2枚目じゃダメな理由教えてくださるとものすごく助かります…… 正しい 4

ケトンやアルデヒドには水素が付加(というか還元される)しますが、カルボン酸には水素は付加しないのですか？理由も教えてくだ 5

光電効果(光電吸収)とは

光電効果とは次のような現象のことを指します。光電効果を光電吸収ということもあります。
光電効果(光電吸収)とは
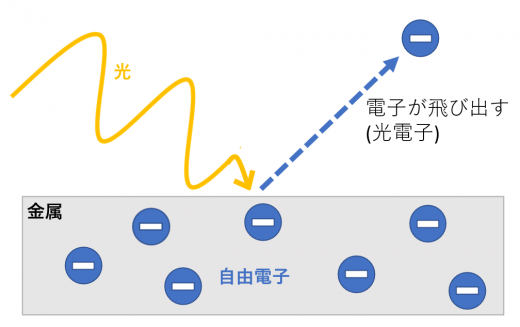
物質にある波長を持つ光が当たると, 電子が飛び出す現象。
ただし, 電子を飛び出させるためには、ある一定以上の光のエネルギーが必要となる。
ここで重要な点は,
ポイント1 : 電子が飛び出す
ポイント2 : ある一定以上の光のエネルギーが必要
の二つです。
飛び出した電子を光電子といいます。
次に, 光電効果が観測できる実験の例を解説します。

光電効果がわかる箔検電器の実験

光電効果がわかる箔検電器の実験について解説します。
上の図において, 上部の金属板に静電気を使いマイナスの電気を与えると, 下部の金属箔まで電子が移動し, マイナスの電気の反発力で金属箔が開きます。
ここで, 上部の金属板にある波長の光を照射すると, 下部の金属箔が先ほどよりも閉じていきます。
この実験事実を次のように解釈します。
光が当たると, 上部の金属板にある電子が飛び出します。
下部の金属箔から上部の金属板に電荷の移動が起こります。
金属箔の反発力が弱まり, 箔が閉じていきます。
1.における電子の飛び出しを光電効果といいます。
次に, 上記の箔検電器の実験の条件を変えて実験を行うことで、「一定のエネルギーの必要性」と, 光の粒子性について解説していきます。
光電効果は光の波長に関係するさて, 箔検電器の実験において, 光の明るさ(強さ)を変えずに、与える光の波長を変えて再実験をします。
まず, 適当な波長の光を使って, 光電効果が起きる条件を用意します。(上図)
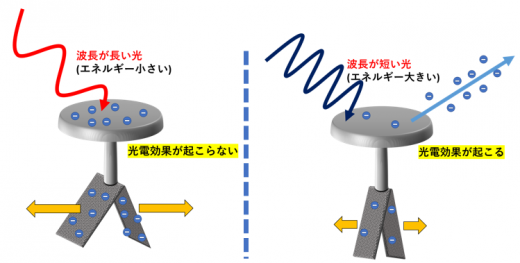
実験1 : 光の明るさは変えずに波長を長くし, 再実験をする, 光電効果が起きません(左図)。
実験2 : 光の明るさは変えずに、波長を短くし, 再実験をすると, 光電効果は起きます(右図)。
この実験でから, 光電効果は短い波長の方が起きやすいことがわかりました。
実際に, 波長が長いものから徐々に短くしながら実験を行うと, ある一定の波長より短い場合は必ず光電効果が起きます。
波長とエネルギーの関係性波長とエネルギーには, 以下のような関係があります。
波長とエネルギーの関係
E=hν=hcλ
E = hν =\dfrac{hc}{λ}
E=hν=λhc​
hhh : プランク定数
ννν (ニュー) : 振動数
λλλ (ラムダ) : 波長
この関係式より, 波長が短いほどエネルギーが大きいことがわかります。
上記の実験において,ある波長よりも短い波長で光電効果が確認されました。
波長とエネルギーの関係を踏まえると, 光電効果を起こすにはある一定以上のエネルギーが必要であるといえます。
光の明るさは光電効果に関与しない今度は, 光の波長を固定し、光の明るさ(強さ)をパラメータとして実験を行います。
光電効果が起こる短い波長において, 光を暗く(弱く)しても光電効果は起こります。
光をどんなに暗くしても光電効果は起こります。(上図)
逆に, 光電効果が起こらない長い波長において, 光を明るく(強く)しても光電効果は起こりません。
光をどんなに光を明るくしても光電効果は起こりません。{(上図)
上記の結果から, 光電効果には光の明るさ(強さ)は関与しないことがわかりました。

光電効果から導かれる光の粒子性

「光=波」→エネルギーと明るさは相関があるはずここで光は単純な波である(光の波動説)と仮定し, 光電効果について考えます。
光を一定の波であるとすれば, 波の振幅は光の明るさ(強さ)と相関があります。つまり, 明るい光は振幅が大きく, 暗い光は振幅が小さくなります。
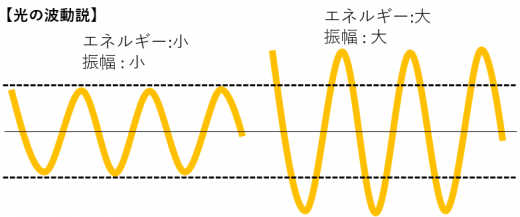
振幅が大きいほどエネルギーが大きいため, 光を明るくすれば光電効果は生じるはずです。
しかし、実際の実験結果は、光電効果は光の明るさに左右されないものでした。
当時の科学者は, 光を単純な波と考えると光電効果を説明できないことに頭を悩ませたそうです。
「光＝粒子」→光電効果は説明可能ここで, 光は粒子の集合体(光の粒子説)であると考えます。
光の粒子の一つ一つがエネルギー(特有の波長または振動数)を持つと考えることができます。
光電効果において, 粒子一つが金属板に与えるエネルギーを衝撃と考えるとイメージがしやすいと思います。
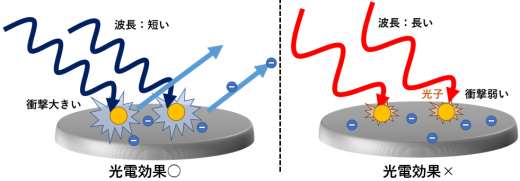
波長が短い粒子はエネルギーが大きく, 金属板上に与える衝撃が大きいため、電子をはじき出すことができ, 光電効果が起きる。(左図)
波長が長い粒子はエネルギーが小さく, 金属板に与える衝撃が小さいため、光電効果が起きない。(右図)
光を粒子と考えた場合、光の明るさは粒子の数に依存します。
波長が長い場合は、粒子の数を増やしても、一つ一つの粒子が与える衝撃は変わらないため、光電効果は起きません。

光電子のエネルギー保存則と仕事関数

光電効果の現象を式で表すと, 以下のような保存則で表現できますす。
光電効果における1個の光る光電子のエネルギー保存則
hν=12mv2+W
hν = \dfrac{1}{2} mv^2 + W
hν=21​mv2+W
ννν (ニュー) : 与えられた光の振動数
vvv : 飛び出した電子の速度
WWW : 仕事関数
右辺の第1項は飛び出した電子の運動エネルギーを表しており、以下のようにも表現されることがあります。
KM=12mv2
K_M=\dfrac{1}{2} mv^2
KM​=21​mv2
保存則において, 左辺は与えられた光のエネルギー、右辺は飛び出す電子のエネルギーの総和を表しています。
仕事関数は光電効果が起きる条件仕事関数とは
hν=12mv2+W
hν = \dfrac{1}{2} mv^2 + W
hν=21​mv2+W
上式における WWWは仕事関数と呼ばれ、電子が飛び出すか飛び出さないかを表現しています。この値は金属の種類によって異なります。
与えられた光のエネルギーhνhνhν が仕事関数WWW よりも大きければ光電効果が起きます。
大学で習う表現ですが, 電子が飛び出ない状態を「束縛されている」といいます。
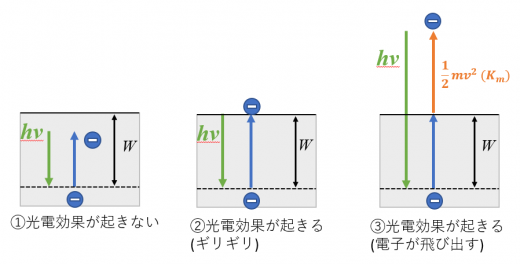
与える光のエネルギーhνhνhνと, 仕事関数WWWは以下のような関係があります。
①hν<Whν<Whν<W : 電子が束縛されており、光電効果は起きません。
②hν=Whν=Whν=W : ギリギリ光電効果は起きます。
③hν>Whν>Whν>W : 光電効果により電子が飛び出す。飛び出した電子は12mv2(KM)\dfrac{1}{2} mv^2(K_M)21​mv2(KM​) のエネルギーを持つ。
仕事関数と限界振動数光電効果は与える光の振動数(波長)が重要です。
限界振動数とは
光電効果が起こるギリギリの振動数を限界振動数ν0ν_0ν0​ といいます。
限界振動数は金属の種類によって異なります。
また, このときの波長を限界波長λ0λ_0λ0​といいます。
与える光の振動数ννν と限界振動数ν0ν_0ν0​ を用いると, 光電効果が起きる条件は以下のようになります。
ν≥ν0ν ≥ ν_0ν≥ν0​  : 光電効果が起きる。
ν<ν0ν < ν_0ν<ν0​  : 光電効果が起きない。
ある金属について, 保存則hν=12mv2+Whν = \dfrac{1}{2} mv^2 + Whν=21​mv2+W と限界振動数ν0ν_0ν0​ をグラフにすると、下図のようになります。
仕事関数, 限界振動数, 限界波長の関係仕事関数, 限界振動数, 限界波長のどれか一つの値がわかれば、その他の値を算出することができます。
上で示した亜鉛ZnとアルミニウムAlについて, 各値を算出してみます。


仕事関数 W[J]W\mathrm{[J]}W[J]
仕事関数 W[eV]W\mathrm{[eV]}W[eV]
限界振動数 ν0[Hz]ν_0\mathrm{[Hz]}ν0​[Hz]
限界波長 λ0[m]λ_0\mathrm{[m]}λ0​[m]


亜鉛 Zn
5.38×10−195.38 \times 10^{-19}5.38×10−19
3.633.633.63
8.11×10148.11\times10^{14}8.11×1014
3.70×10−73.70\times10^{-7}3.70×10−7

アルミニウム　Al
6.72×10−196.72\times10^{-19}6.72×10−19
4.204.204.20
1.01×10151.01\times10^{15}1.01×1015
2.97×10−72.97\times10^{-7}2.97×10−7

以下の各値の算出方法を明記します。
仕事関数 W[eV]W\mathrm{[eV]}W[eV] の単位変換
→　1eV=1.60×10−19[J]1 \mathrm{eV}= 1.60×10^{-19} \mathrm{[J]}1eV=1.60×10−19[J] の関係から W[J]W\mathrm{[J]}W[J] を電荷 eee で割る。
限界振動数ν0[Hz]ν_0\mathrm{[Hz]}ν0​[Hz]の導出
→ W=hνW = hνW=hν の関係から W[J]W\mathrm{[J]}W[J] をプランク定数 hhh で割る。
※[J]\mathrm{[J]}[J]の単位に注意, h=6.63×10−34[J⋅s]h = 6.63 \times 10^{-34}\mathrm{[J \cdot s]}h=6.63×10−34[J⋅s]
限界波長λ0λ_0λ0​ の導出 →　λ0=cν0λ_0 = \dfrac{c}{ν_0}λ0​=ν0​c​ の関係から求められる。
(補足：光速 c=3.0×108[m/s]c = 3.0×10^{8}\mathrm{[m/s]}c=3.0×108[m/s] )
阻止電圧とは最後に, 阻止電圧について考えてみます。
適当な振動数の光を陰極の金属板に当て、光電効果を起こします。(上図)
このとき, 図②のように陽極と陰極間に電圧をかけ電場を発生させます。そうすると, 光電子の運動が電場によって妨げられ, 光電子の運動エネルギーが小さくなります。
さらに電圧を大きくすると, 電子の運動エネルギーと阻止電圧のエネルギーが釣り合うことで, 電子が飛び出なくなります。
このときの電圧を阻止電圧といいます。
阻止電圧V0V_0V0​がわかることで, 飛び出した電子の運動エネルギーがわかるわけです。与えた光のエネルギーがわかっていれば, 仕事関数も求められます。
つまり、次のようなエネルギー保存則が成り立ちます。
KM=hν−W=eV0
K_M =hν - W= eV_0
KM​=hν−W=eV0​

	仕事関数 $W\mathrm{[J]}$	仕事関数 $W\mathrm{[eV]}$	限界振動数 $ν_0\mathrm{[Hz]}$	限界波長 $λ_0\mathrm{[m]}$
亜鉛 Zn	$5.38 \times 10^{-19}$	$3.63$	$8.11\times10^{14}$	$3.70\times10^{-7}$
アルミニウム　Al	$6.72\times10^{-19}$	$4.20$	$1.01\times10^{15}$	$2.97\times10^{-7}$

身近な光電効果の応用例

以上のような光電効果は, 私たちの身近に応用例があります。

例えば, スマートフォンや家電に欠かすことができない半導体, 再生可能エネルギーのための太陽光発電のパネルです。

他にもノーベル賞を受賞した小柴昌俊博士の研究で有名なカミオカンデの光電子倍増管があります。

また, 私たちの目で夜空に遠い星が観察できることは、光の粒子性が関係あるそうです。気になる方は調べてみてください。

「光＝波」考えられてた常識を打ち破った光電効果の発見は, 人類にとって大きな一歩です。