ミリカンの油滴実験を用いた電気素量の求め方

帯電体(電気を帯びた物質)が持つ電気量の大きさは, 素電荷 $e$ の整数倍となります。

なぜならば, 電子が素粒子(分割できない最小単位)であり, 帯電体の電気量の大きさは電荷の個数に比例するからです。電荷の個数は必ず整数をとります。

$e ≒ 1.60×10^{-19} \mathrm{[C]}$ という数字は暗記しておくことをお勧めします。

原子を分解すると素粒子になる

上記で扱った素粒子について簡単に説明します。

物質を分解していくと, 元素表に載っているような原子に分割できます。そして, 原子は原子核と電子にわけられます。

原子核は, 陽子と中性子に分割することができます。しかし, 電子はそれ以上に分割できません。

さらに, 陽子と中性子はクォークと呼ばれる粒子にわけること可能です。正確に言えば,

• 陽子：アップクォーク2個＋ダウンクォーク1個
• 中性子：アップクォーク1個, ダウンクォーク2個

にわけられます。

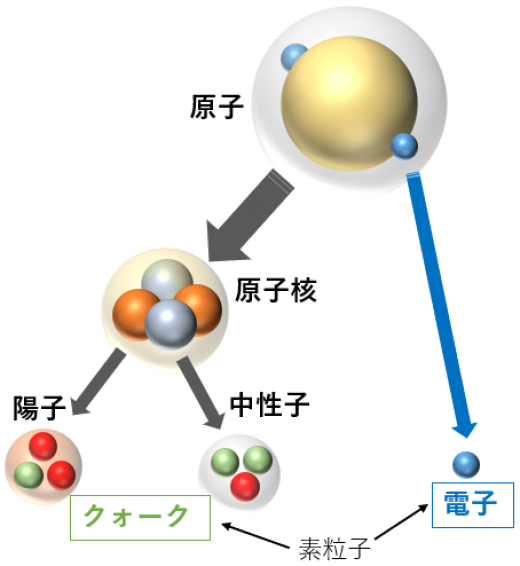
このクォークはそれ以上に分割できません。電子やクオークのようにそれ以上に分割できない粒子を素粒子といいます。

素粒子は物質の最小単位

素粒子は物質の最小単位で, 宇宙の起源に大きく関わっており, 今も研究が進められています。

ヒッグス粒子の発見やニュートリノの質量観測などニュースで聞いたことがあるかもしれません。

電気素量 $e = 1.6×10^{-19}$ を実験的に求めたのが ミリカンです。ミリカンが行った「油滴の実験」は非常に有名な実験です。

ミリカンは1923年に電気素量の発見と光電効果の研究によりノーベル賞を受賞しています。

→光電効果

次から電気素量の発見に繋がった「油滴の実験」について解説していきます。

ミリカンの油滴の実験

ミリカンは下図のような実験装置を準備しました。

油を入れた霧吹きで作った油滴が落下する様子を顕微鏡で観察し, 油滴が落ちる速度を測定できます。また, 落ちていく油滴にX線を照射することも可能です。

そして, ミリカンは極板間に

1. 電圧をかけない場合
2. 電圧をかける場合

を比較することで電気素量を求めることに成功しました。順を追って, その手順を説明していきます。

1. 電圧をかけない場合

まず, 電圧をかけずに油滴の落下を観察します。

1. 霧吹きで小さな油滴を作り, 上部の極板中央の小さな穴から油滴を落下させます。

2. 空気中にX線を照射し, 空気分子をイオン化させます。→ イオン化した空気分子が油滴に付着し, 油滴が帯電します。

3. 落下する油滴は軽い重力を加速します。→ しかし, 油滴は非常に軽いため空気抵抗を受け, 終端速度(等速)で落下します。

4. この終端速度$v_0$を顕微鏡で見ながら測定します。

終端速度を復習したい方は以下を参照してください。

→終端速度

重力と空気抵抗のつり合いを考える

電圧をかけない場合は, 油滴一つに関して下図のように, 力が釣り合います。

式で表すと,

$$mg = k v_0$$

となります。パラメータは以下の通りです。

$m$ [$\mathrm{kg}$] : 油滴の質量

$g$ [$\mathrm{m/s^2}$] : 重力加速度

$k$ : 空気抵抗の比例定数

$v_0$ [$\mathrm{m/s}$] : 電圧をかけない場合の終端速度

今回, 浮力は空気抵抗力に比べ非常に小さいものとして無視しています。

油滴は一つ一つの大きさ(体積)が異なるため, $m$ がバラバラなことに注意してください。

空気抵抗定数 $k$ の算出

油滴の実験では終端速度 $v_0$ が測定可能です。重力加速度 $g$ は既知であり, $m$ と $k$ は未知数になります。

油滴の質量 $m$ は油滴の密度 $\rho$ と半径 $r$ を使って算出することができます。一つの油滴が半径 $r \mathrm{[m]}$ の綺麗な球形をしていると仮定すると, 体積 $V = \dfrac{4}{3} \pi r^3$[$\mathrm{m^3}$]となります。

油滴の密度を$\rho [\mathrm{kg /m^3} ]$ とすると, 油滴の質量は,

$$m = \dfrac{4}{3} \pi r^3 \rho$$

と表現できます。

よって, 油滴の実験において油滴の半径 $r\mathrm{[m]}$ を測定できれば, 質量$m \mathrm{[kg]}$ が既知の値になります。

したがって, つり合いの式を変形させた以下の式から, $k$ が求められます。 $$k = \dfrac{mg}{v_0}$$

2. 電圧をかける場合

次に, 上記と同じ手順で電圧をかける場合について考えます。

電場 $E$ をとすると, 帯電した油滴に $qE$ という力がかかります。そして, 帯電した油滴は電場の向きと強さによって, ①上昇　②静止 ③下降の3パターンが存在します。

今回は, 鉛直上向きに適当な $E$ をかけ, 下図のように油滴が空中で静止させた場合について考えます。

油滴が電場によって上下に運動する場合は後述します。

図のように油滴を静止している時, 鉛直下向きの重力 $mg$ と鉛直上向きの電場から受ける力$qE$ がつりあっています。式で表すと,

$$mg = qE$$

となります。

$q \mathrm{[C]}$ : 油滴の電気量の大きさ

$E\mathrm{[V/m]}$ : 極板間の電場の強さ

電圧をかけて油滴を運動させる場合

電場の向きと大きさを調整し, 油滴が上昇または下降する場合について考えます。このとき, 終端速度を使いって, 以下のようなつり合いの式をたてることができます。

[油滴が上昇する場合(右図)]

$$mg = qE + kv_1$$

$v_1 \mathrm{[m/s]}$ : 油滴が上昇する終端速度

[油滴が下降する場合(左図)]

$$mg + qE = kv_2$$

$v_2 \mathrm{[m/s]}$ : 油滴が下降する終端速度

この場合終端速度$v_1$と$v_2$を測定する必要があります。

油滴実験を使った電気素量の求め方

今回は, 電圧をかけない場合と電圧をかけ油滴を静止させた場合を使って 油滴の電気量 $q$ を求めます。

[電圧をかけない場合] $$mg = k v_0$$

[電圧をかけ, 油滴を静止させた場合] $$mg = qE$$

2つのつり合いの式から, 油滴の電気量 $q$ を求めると,

$$q = \dfrac{k v_0}{E}$$

が得られます。

$v_0$ は測定から, $k$は前節で示した計算から求めることができます。$E$ は実験条件からわかるため, $q$を割り出すことができます。

ただし, この $q$ を求めただけでは, 電気素量は求まっていません。 なぜならば, 油滴一つに電荷が何個も含まれているからです。

$e = 1.60×10^{-19}$ は経験的に求められた

ミリカンは素電荷を求めるために, 油滴実験を何度も行い, $q \mathrm{[C]}$ をたくさん求めました。

ミリカンは $q \mathrm{[C]}$ をたくさん求めることである法則性を見つけます。それは, $q$ [C] がある値の整数倍となっているということです。

その値というのが,

$$1.60×10^{-19}$$

です。この事実は, 油滴の電気量$q$ [C]は電気素量 $e$ が電荷の個数分の値であることを示しています。

これにより, $e ≒ 1.60×10^{-19}\mathrm{[C]}$ が電気量の最小単位である電気素量であることがわかりました。

$q\mathrm{[C]}$ が $e$ の整数倍であることは次の例題1を解けば, より理解が深まると思います。

ミリカンの実験を使った例題に以下のようなものがあります。