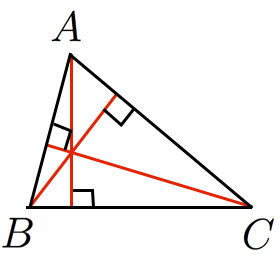
定理2

三角形
ABC
の外心を
O
として,AO
と
BC
の交点を
D
とおく(E,F
も同様)
すると,AD1+BE1+CF1=R2
まずは,定理1の証明1と同様に計算で証明します。三角形
ABC
の情報で
AD
を求めに行きます。
証明1
三角形
ABD
に正弦定理を用いると,
sinBAD=sin∠ADBc
ここで
O
から
AC
に下ろした垂線の足を
H
とおくと
∠AOH=∠B
より
∠DAC=90∘−B
である。
よって,∠ADB=∠DAC+C=(90∘−B)+C
であるので
AD=cos(B−C)csinB
さらに正弦定理と加法定理を用いて角度のみの情報にする:
AD1=2RsinBsinCcosBcosC+sinBsinC=2R1(1+tanBtanC1)
BE1,CF1
も求まるので
右辺は,
2R1(3+tanAtanB1+tanBtanC1+tanCtanA1)=R2
ただし,最後の等号はタンジェントの美しい関係式を用いた。
次は,三角形の面積に注目した証明です。
証明2
三角形 AOB,BOC,COA の面積をそれぞれ SC,SA,SB とおく。
S:S−SA=AD:AO=AD:R
より AD=S−SASR
同様に BE=S−SBSR,CF=S−SCSR
よって
AD1+BE1+CF1=SR(S−SA)+(S−SB)+(S−SC)=SR2S=R2