弧度法の意味と度数法に対するメリット
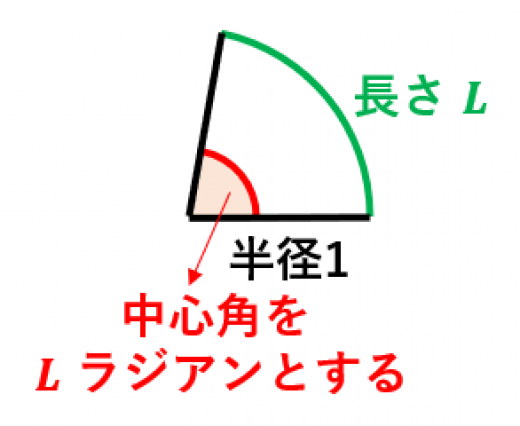
弧度法とは「半径が で弧の長さが である扇形の中心角を ラジアンとする」ような角度の表し方。
- 弧度法の意味と公式について詳しく解説します。
- なぜ度数法ではなく弧度法を使うと嬉しいのか?弧度法を使うメリットも解説します。
弧度法と度数法の意味
弧度法と度数法の意味
弧度法とは
- 弧度法とは「半径が で弧の長さが である扇形の中心角を ラジアンとする」ような角度の表し方です。
-
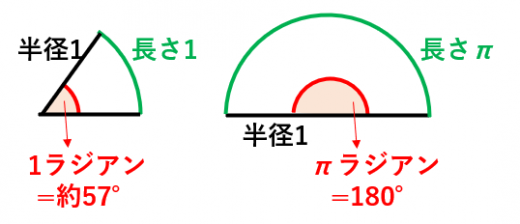
例えば「半径も弧の長さも1である扇形の中心角」が1ラジアンです。
-
また,半径が1の半円の周の長さは なので,半回転分= ラジアン になります。
-
高校数学以降では弧度法を使うことが多いです。
度数法とは
- 弧度法に対して,おなじみの という角度の表し方を「度数法」と言います。
- 度数法では,半回転分= となります。「1回転分=360°」です。
弧度法と度数法の変換
弧度法と度数法の変換
半回転分は,度数法では ,弧度法では ラジアンでした。つまり, ラジアンです。これを使うと,「度」と「ラジアン」を互いに変換できます。
「度」を「ラジアン」に変換する方法:
度に をかけるとラジアンに直せます。
を弧度法で表すと, ラジアン
「ラジアン」を「度」に変換する方法:
ラジアンに をかけると度に直せます。
ラジアンを度数法で表すと,
弧度法の覚え方
度数法と弧度法の対応の覚え方は,やはり上述されているように,「 ラジアン」が最も素直で覚えやすいと思います。
何問か度数法を弧度法に変換する例題を解くことで,覚えやすくなると思います。
弧の長さの公式
弧の長さの公式
半径
,中心角
ラジアンの扇型の弧の長さは
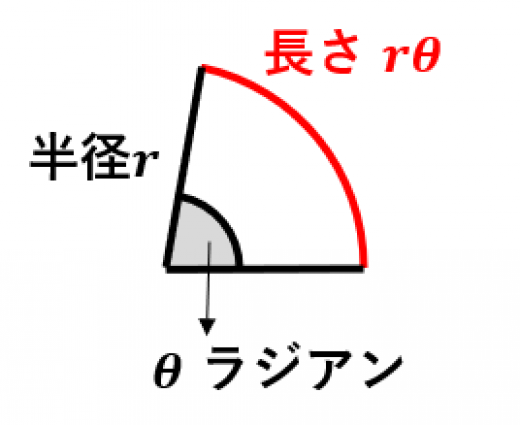
例えば,半径が で中心角が ラジアンである扇形の弧の長さは, と計算できます。
弧度法において弧の長さが になることを2通りの方法で説明します。
弧度法の定義より,半径1,中心角 ラジアンの弧の長さが であった。半径を 倍にすると弧の長さも 倍になるので, が弧の長さになる。
度数法では,半径 ,中心角 の扇型の弧の長さは であった。一方, ラジアンは 度なので,上記で とすると,弧の長さは となる。
扇形の面積公式
扇形の面積公式
半径 ,中心角 ラジアンの扇型の面積は
例えば,半径が で中心角が ラジアンである扇形の面積は, と計算できます。
弧度法において扇形の面積が になることを証明します。
度数法では,半径 ,中心角 の扇型の面積は であった。一方, ラジアンは 度なので,上記で とすると,扇形の面積は となる。
弧度法を使うメリット
弧度法を使うメリット
ここからが本題です。度数法ではなくわざわざ弧度法を使うのはなぜか考えてみます。
-
弧の長さ,面積がシンプル: 上記の「弧の長さと面積の公式」を見ると度数法よりも弧度法の方がややシンプルです。これは弧度法の利点です。しかし,この程度では「度数法よりも弧度法の方が優れている」という強い理由にはならないと思います。
-
三角関数の極限,微分などの操作がシンプル: 弧度法の本当の嬉しさを理解できるのは,数学3で三角関数の極限を習ってからです。以下では,この嬉しさについて理解するために,度数法の場合と弧度法の場合を比較してみます,弧度法の存在意義を実感して下さい!
弧度法だと美しい
弧度法だと美しい
弧度法の利点を端的に言うと 公式1の美しさです。
公式1:正弦の極限公式:
公式2:三角関数の微分:
公式3:正弦のマクローリン展開:
1の証明は,sinx/xについて覚えておくべき2つのことの中盤にあります。1を使うことで2が証明できます。
さらに2を使ってサインの高階導関数が求まり,3が導出できます。公式3は高校数学の範囲外ですが知っておくとよいです。 →マクローリン展開
度数法だと美しくない
度数法だと美しくない
上記の3つの公式について,度数法の世界で考えると以下のようになります。
公式1:正弦の極限公式:
公式2:三角関数の微分:
公式3:正弦のマクローリン展開:
証明自体は弧度法の場合と全く同様にできますが,結果は非常に汚くなります(特に公式3)。弧度法の場合の方が断然美しいですね。
つまり,度数法よりも弧度法が本質的に優れているという訳ではありませんが,度数法を使うと比例定数 がいろいろなところに出現してとてもめんどうなので弧度法を使うのがよい,と言えます。
文系の人は数学3を習わないので,弧度法の素晴らしさを理解できないまま弧度法を使わざるを得ないということになります。











