sin、cos、tan の意味
sin, cos, tan(三角比・三角関数)について基礎からわかりやすく説明します。
sin, cos, tan の意味【基本】
sin, cos, tan の意味【基本】
(図のように を含む直角三角形を描いたもとで)
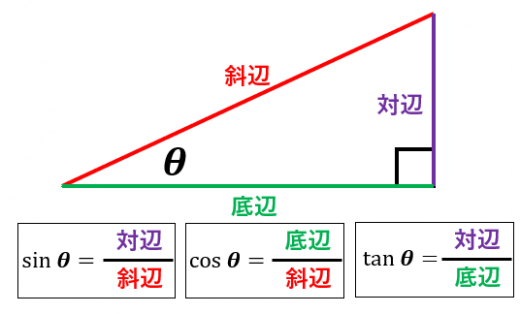
- とは 対辺の長さ/斜辺の長さ のこと
- とは 底辺の長さ/斜辺の長さ のこと
- とは 対辺の長さ/底辺の長さ のこと
つまり, で1つの数を表します。
例えば について考えます。
を含む直角三角形は,右上も になるので二等辺三角形です。
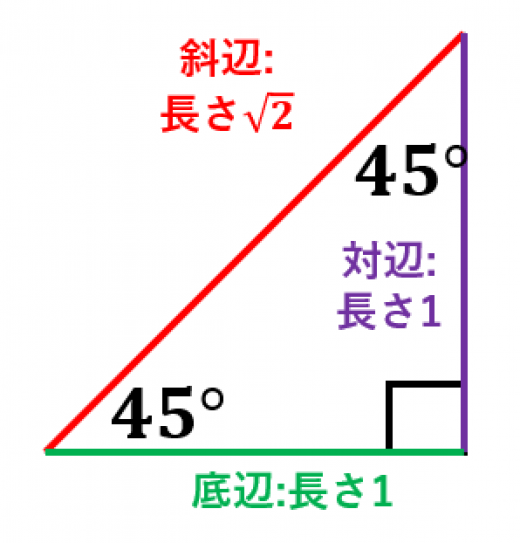
底辺と対辺の長さを1とすると,三平方の定理より斜辺の長さは となります。
よって, となります。
同じように,, です。
覚え方
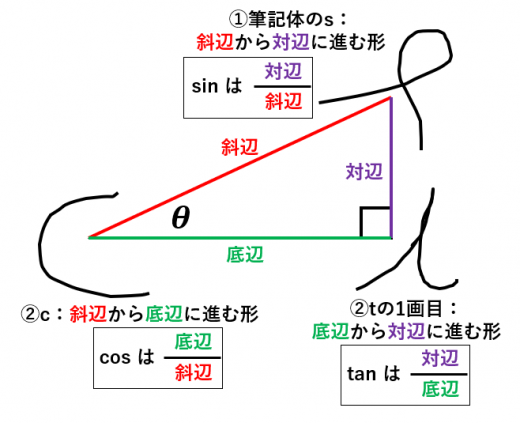
① は「s」の筆記体で覚えましょう。
② は「c」で覚えましょう。
③ は「t」で覚えましょう。
と と をそれぞれ求めよ。
を含む直角三角形は「正三角形の半分」。よって斜辺の長さを2とすると底辺は1。対辺の長さは三平方の定理より
よって,,,
三角比の表
三角比の表
上の練習問題を元に三角比の表を作ってみましょう。
計算方法をしっかり覚えて上の表を埋められるようにしましょう。
マイナスや90°以上の場合のsin,cos,tan
マイナスや90°以上の場合のsin,cos,tan
一般角
- の場合は,さきほどみたように直角三角形を使って が定義されました。
- がマイナスの場合や, 以上の場合は,円を使って定義されます。
任意の実数 に対して
軸の正の部分を原点中心に反時計回りに だけ回転させた半直線と単位円の交点の座標を と定義する。

また( のもとで), と定義する。
の場合,この定義は,さきほどの直角三角形による定義と一致します。
関連する用語
関連する用語
弧度法
-
角度を表すときに,数学II以降では「度」より「ラジアン」を使うことが多いです。
-
と書かずに と書くことが多いです。
-
ラジアン(弧度法)については弧度法の意味と度数法に対するメリットで詳しく解説しています。
三角比・三角関数
- のことをまとめて三角比と呼びます。
- を入力として値を返す関数とみなせるので三角関数と呼ぶこともあります。
- 数学Iでは三角比,数学II以降では三角関数と呼ぶことが多いです。あまり区別する必要はありません。
読み方
- は「サイン」
- は「コサイン」
- は「タンジェント」
- は「シータ」です。角度を表すのによく使うギリシャ文字です。数学と物理におけるギリシャ文字の使い方一覧
sin, cos, tanの応用例
sin, cos, tanの応用例
三角関数を習いたてだと
「三角関数は何の役に立つのか? なぜ三角関数を学ぶのか?」と思うかもしれません。
三角関数を学ぶのは単に入試の役に立つだけではなく社会の役に立つからです。例えば,
-
測量:角度から長さを求めたり,長さから角度を求めるのに使えます。
-
物理現象の記述:例えば電気回路や振り子の計算でsin,cosが登場します。
-
ゲーム制作:例えば物体を回転させた位置を計算するのに使えます。
-
音波など波の分析:フーリエ級数展開・フーリエ変換という分野でsin,cosが登場します。
私も習いたてのころは「1つの数を表すのに などと4文字も使って長いなあ,何の役に立つか分からない」と思っていました。











