直角三角形の定義とさまざまな公式
直角三角形とは,1つの角が直角である三角形のことです。
直角三角形のさまざまな性質を紹介します。
三平方の定理(ピタゴラスの定理)
三平方の定理(ピタゴラスの定理)
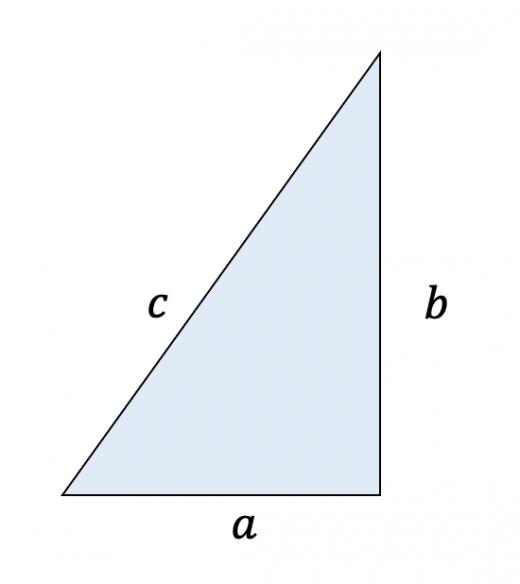
直角三角形において,
つまり「斜辺以外の二辺の長さの二乗の和」は「斜辺の二乗」と等しい。
は直角三角形の3辺の長さで, が斜辺です。
補足:ピタゴラス数(整数の話題)
一般に,三つの自然数の組 が三平方の定理の式 を満たすとき, をピタゴラス数と呼びます。
有名なピタゴラス数として, や があります。実際 などが成立します。
また,ピタゴラス数は「とある公式」を用いることで「すべて」作り出せます。ピタゴラス数の性質についてはこちらの記事で詳しく扱っています。→ピタゴラス数の求め方とその証明
有名な直角三角形と辺の長さの比
有名な直角三角形と辺の長さの比
直角三角形の中でも,特に有名で大事なものを紹介します。
ピタゴラス数と関係する直角三角形
- 三辺の長さが の直角三角形
- 三辺の長さが の直角三角形
これらは,3辺の長さがすべて整数(ピタゴラス数)であるため,有名です。
角度の大きさがきれいな直角三角形
角度が特徴的であるために有名な三角形もあります。
-
三つの角が である直角三角形。
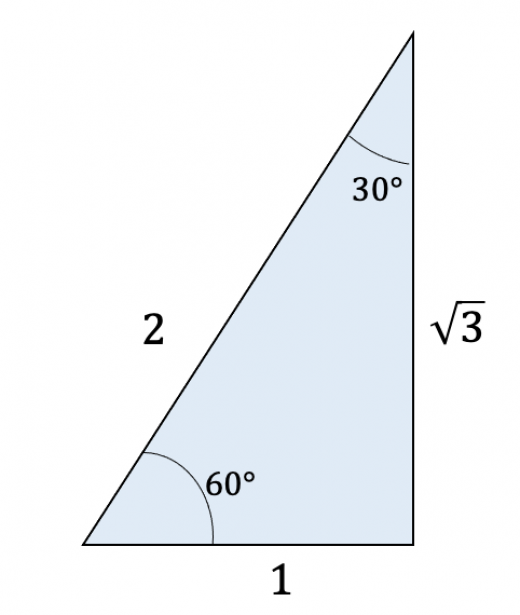 三辺の比が となります。正三角形を半分に切った直角三角形です。
三辺の比が となります。正三角形を半分に切った直角三角形です。 -
三つの角が である直角三角形。
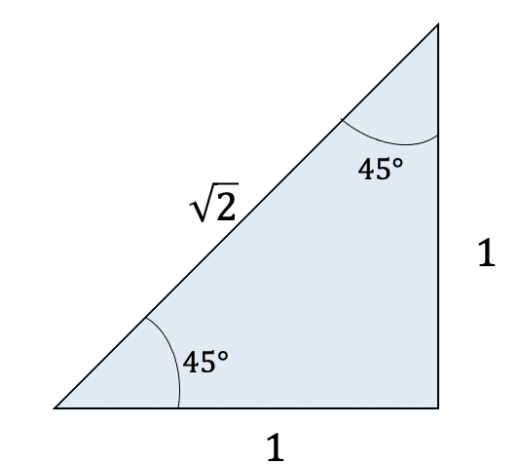 直角二等辺三角形です。三辺の比が となります( です)。
直角二等辺三角形です。三辺の比が となります( です)。
円の直径と直角三角形
円の直径と直角三角形
円周上にある3点 を頂点とする三角形 について,1辺が円の直径と一致するなら, は直角三角形。
円周角の定理を用いて簡単に証明できます。
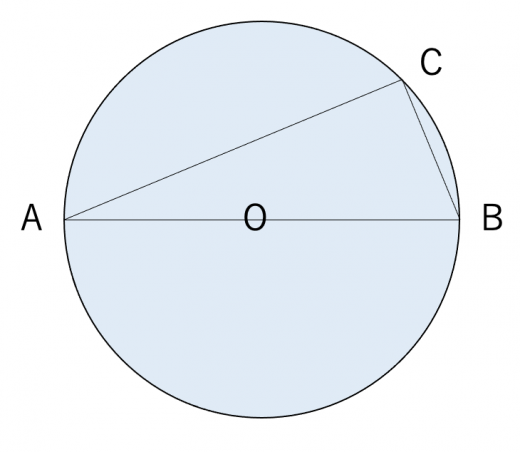 が直径と一致する場合を考える。
が直径と一致する場合を考える。
このとき であるから,円周角の定理より
つまり,三角形 は直角三角形。
この性質はタレスの定理とも呼ばれます。「円の直径→直角三角形が潜んでいるかも」と意識しておきましょう。
直角三角形の合同条件
直角三角形の合同条件
直角三角形は,1つの角度が であるため,特有の合同条件を持ちます。
- 斜辺と1つの直角でない角が等しいなら合同
- 斜辺ともう1辺がそれぞれ等しいなら合同
斜辺と1つの直角ではない角が等しい場合,直角三角形において直角でない二つの角の大きさの和は なので、全ての角の大きさが等しい。
つまり,斜辺とその両端の角が等しいことになるので,2つの三角形は合同である。
斜辺ともう1辺がそれぞれ等しい場合を考える。
 とする。このとき, と をくっつけてできる三角形 は二等辺三角形となる。
とする。このとき, と をくっつけてできる三角形 は二等辺三角形となる。
よって, であり,2つの直角三角形は斜辺と1つの直角でない角が等しい。このとき二つの三角形が合同となることについては,1で証明した。
よって,二つの三角形は合同である。
直角三角形と三角関数
直角三角形と三角関数
直角三角形は,三角関数 の定義に使われることがあります。
 である以上のような三角形において,
である以上のような三角形において,
直角三角形に慣れ親しんでおけば,三角関数も理解しやすいです。










