三角関数のグラフの特徴と簡単な書き方

更新 2022/02/28

この記事では三角関数のグラフの書き方を説明します。物理でも正弦波として頻出です。是非おさえておきましょう。

sin と cos のグラフ

まず，sin⁡θ,cos⁡θ\sin\theta,\cos\thetasinθ,cosθ の意味を確認しましょう。角 θ\thetaθ の動径と単位円の交点 P\mathrm{P}P の xxx 座標，yyy 座標がそれぞれ cos⁡θ,sin⁡θ\cos\theta ,\sin \thetacosθ,sinθ でした。
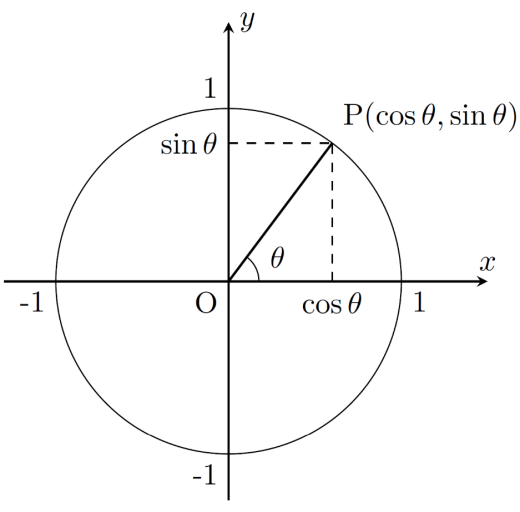
この定義に基づいて y=sin⁡xy = \sin xy=sinx のグラフと y=cos⁡xy = \cos xy=cosx のグラフを描くと，下の図の右側のようになります。
y=sin⁡xy = \sin xy=sinx のグラフと y=cos⁡xy = \cos xy=cosx のグラフは「同じ形」ですね。実際，sin⁡(x+π2)=cos⁡x\sin \left(x + \dfrac{\pi}{2} \right) = \cos xsin(x+2π​)=cosx であることから，y=cos⁡xy = \cos xy=cosx のグラフは y=sin⁡xy = \sin xy=sinx のグラフを π2\dfrac{\pi}{2}2π​ だけ平行移動させたものだとわかります。
y=sin⁡xy=\sin xy=sinx や y=cos⁡xy = \cos xy=cosx の形をしたグラフを正弦曲線といいます。
上のグラフを見ると「同じ形」が連続しています。実際，sin⁡(x+2π)=sin⁡x\sin (x + 2\pi) = \sin xsin(x+2π)=sinx なので，正弦曲線は 2π2\pi2π ごとに同じ形を繰り返します。
このように，ある実数 aaa について，f(x+a)=f(x)f(x+a) = f(x)f(x+a)=f(x) となる関数を周期関数といいます。aaa を周期といいます。y=sin⁡xy=\sin xy=sinx や y=cos⁡xy=\cos xy=cosx の周期は 2π2\pi2π です。

tan のグラフ

次は，y=tan⁡xy=\tan xy=tanx のグラフです。P(cos⁡θ,sin⁡θ)\mathrm{P} (\cos \theta , \sin \theta)P(cosθ,sinθ) とおくと，直線 OP\mathrm{OP}OP は y=(tan⁡θ)xy = (\tan \theta) xy=(tanθ)x と表されます。ここで x=1x=1x=1 のとき，y=tan⁡θy = \tan \thetay=tanθ となります。図にすると次のようになります。
θ\thetaθ を動かすことで y=tan⁡xy= \tan xy=tanx のグラフは次のように描かれます。
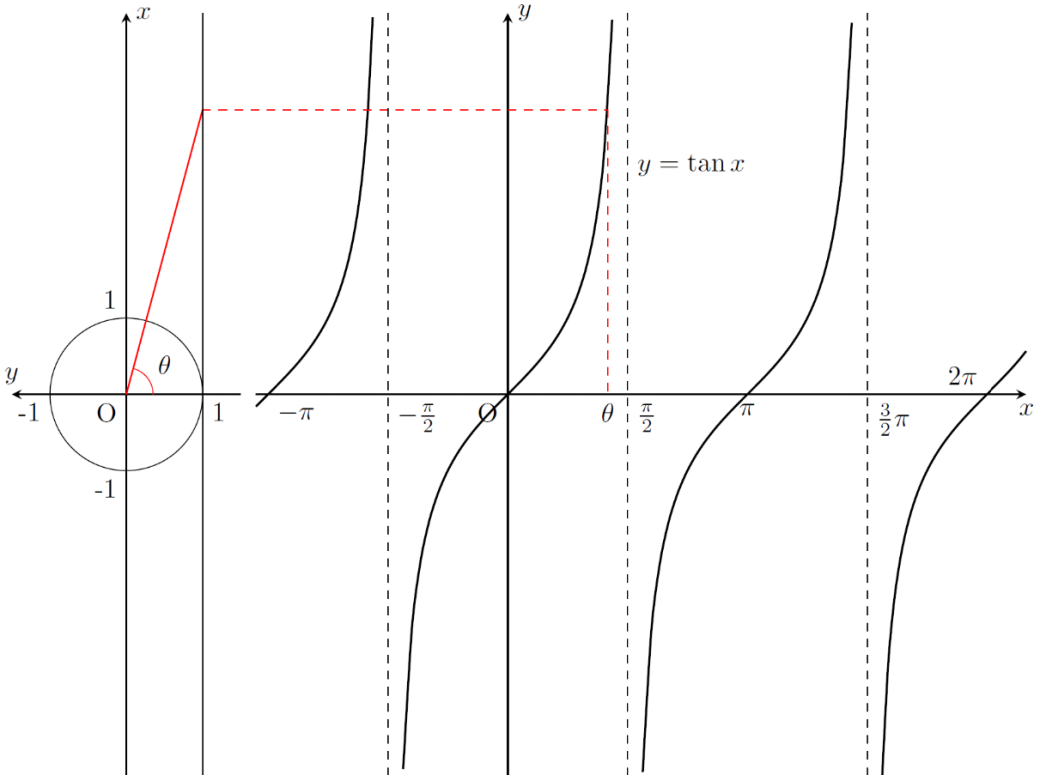
0<x<π20 < x < \dfrac{\pi}{2}0<x<2π​ の範囲で，xxx を π2\dfrac{\pi}{2}2π​ に近付けると tan⁡x\tan xtanx の値は限りなく大きくなっていきます。つまり，y=tan⁡xy = \tan xy=tanx のグラフが直線 x=π2x = \dfrac{\pi}{2}x=2π​ に近付いていきます。このようにグラフがある直線に近付くとき，その直線を漸近線といいます。
y=tan⁡xy = \tan xy=tanx の周期は π\piπ です。実際，tan⁡(x+π)=tan⁡x\tan (x+\pi) = \tan xtan(x+π)=tanx です。
ここまでのまとめ
y=sin⁡x,y=cos⁡x,y=tan⁡xy=\sin x,y=\cos x,y=\tan xy=sinx,y=cosx,y=tanx のグラフの形は覚える
y=sin⁡xy=\sin xy=sinx と y=cos⁡xy=\cos xy=cosx は同じ形で，片方を π2\dfrac{\pi}{2}2π​ 平行移動すると重なる
y=sin⁡xy=\sin xy=sinx と y=cos⁡xy=\cos xy=cosx の周期は 2π2\pi2π，y=tan⁡xy=\tan xy=tanx の周期は π\piπ

様々な正弦曲線

例題

次の式のグラフを描け。

$y = \sin \left( x - \dfrac{\pi}{3} \right)$
$y=2 \sin x$
$y = 2 \sin \left( x - \dfrac{\pi}{3} \right)$
$y = \cos 2x$
$y= \cos \left( x + \dfrac{\pi}{6} \right)$
$y = \cos \left( 2x + \dfrac{\pi}{3} \right)$

正弦曲線の平行移動

$\sin$ のなかが $x$ に定数を足し(引い)ている場合は，元の正弦曲線を平行移動させたものとなります。例えば $y = \sin \left( x - \dfrac{\pi}{3} \right)$ は $y=\sin x$ を $\dfrac{\pi}{3}$ 平行移動した曲線です。そのため本体 $(0,0)$ となるところは $\left( \dfrac{\pi}{3} , 0 \right)$ に移動します。

解答 1

$y = \sin \left( x - \dfrac{\pi}{3} \right)$ と $y=\sin x$ を比較してみましょう。

$y$ 軸方向の拡大

三角関数に定数を掛けたもののグラフは，元々のグラフを縦方向( $y$ 軸方向)に定数倍したものになります。例えば $y= 2 \sin x$ は $y = \sin x$ を $y$ 軸方向に2倍拡大したものとなります。

解答 2

$y=2\sin x$ と $y=\sin x$ を比較してみましょう。

解答 3

3番は1番と2番を組み合わせることで得られます。

$x$ 軸方向の拡大

$y = \cos 2x$ は $y = \cos x$ を $x$ 軸方向に 1/2に縮小したものとなります。また， $x$ 軸方向の拡大では周期が変化します。例えば $\cos 2 (x + \pi) = \cos (2x + 2\pi) = \cos 2x$ となるため，周期が $\pi$ です。一般に $\sin kx , \cos kx$ の周期は $\dfrac{2\pi}{k}$ となります。

解答 4,5

5は平行移動したものです。ただし $-\dfrac{\pi}{6}$ 平行移動していることに気を付けてください。

$x$ 軸方向の拡大と平行移動が組み合わさる場合は，少々複雑になります。

解答 6

$y = \cos \left( 2x + \dfrac{\pi}{3} \right) = \cos 2 \left( x + \dfrac{\pi}{6} \right)$ であるため， $y = \cos 2x$ を $x$ 軸方向に $-\dfrac{\pi}{6}$ 平行移動させたものになる。

$y = \cos \left( 2x + \dfrac{\pi}{3} \right)$ は $x$ 軸方向に $-\dfrac{\pi}{3}$ 平行移動させたものではないです。 $(x - \text{定数})$ の形を作るようにしましょう。

正弦関数を簡単に描く方法

関数を描くときは，目盛りが正確に描かれていれば問題はありません。すなわち次の2つはグラフとしては同じになります。

次のような方法で描くと簡単に描けます。

正弦曲線と $x$ 軸を描く。
平行移動前の原点がどこに移動したのか調べて $y$ 軸を描く。
$y$ 座標の最大最小を調べて書く。
周期を調べて $x$ 軸に目盛りを書く。

実際に $y = \cos \left( 2x + \dfrac{\pi}{3} \right)$ を描いてみましょう。

$2x + \dfrac{\pi}{3} = 2 \left( x + \dfrac{\pi}{6} \right)$ から， $y = \cos 2x$ の原点は $\left( -\dfrac{\pi}{6} , 0 \right)$ に移動します。
$y = \cos \left( 2x + \dfrac{\pi}{3} \right)$ の最大値・最小値は $1$ ， $-1$ です。
周期が $\pi$ であることを考えて目盛りを書きこみます。

正弦曲線は物理において波の分野で頻出します。合わせて勉強しましょう。