どの公式も cos の倍角の公式から導出できます。
sin の半角の公式
サインの半角の公式
sin22θ=21−cosθ
sin の半角の公式の証明
cos の倍角の公式
cos2θ=1−2sin2θ
の θ を 2θ に置き換えて整理すると
sin22θ=21−cosθ
を得る。
cos の半角の公式
コサインの半角の公式
cos22θ=21+cosθ
sin と同様に示すことができます。
cos の半角の公式の証明
cos の倍角の公式
cos2θ=2cos2θ−1
の θ を 2θ に置き換えて整理すると
cos22θ=21+cosθ
を得る。
tan の半角の公式
タンジェントの半角の公式
tan22θ=1+cosθ1−cosθ
これまでの2つを組み合わせるだけです。
tan の半角の公式の証明
tan22θ=cos22θsin22θ=1+cosθ1−cosθ
0<θ<2π の場合,図形的に証明することもできます。
証明
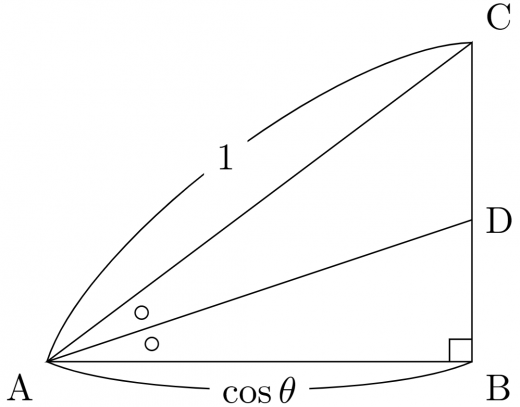
cosθ=∠CAB とする。
AD は ∠CAB を二等分するため,
AB:AC=BD:DC
である。ゆえに
BD=AB+ACABBC=1+cosθcosθBC
よって
tan2θ=ABBD=1+cosθcosθABBC=1+cosθsinθ
である。
辺々を2乗して
tan22θ=(1+cosθ)2sin2θ=(1+cosθ)21−cos2θ=1+cosθ1−cosθ
を得る。
またこの方法によってタンジェントの半角の公式の別の形
tan2θ=1+cosθsinθ
も得られました。












