対偶を用いた証明のいろいろな具体例
「 ならば 」に対して,「 でないならば でない」のことを対偶と言います。
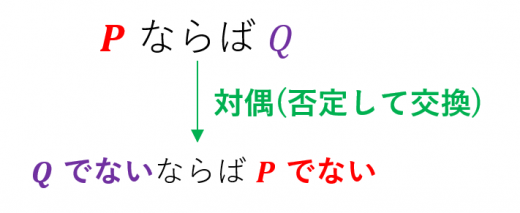
例えば,「数学ならば面白い」の対偶は,「面白くないなら数学ではない」です。
対偶の例
対偶の例
対偶の意味を理解するために,いくつか例を見てみます。
「 が3の倍数ならば, は3の倍数である」
の対偶は,
「 が3の倍数でないならば, は3の倍数でない」
このように,「ならば」の前と後をそれぞれ否定して交換すると対偶になります。
※例1は,どちらも正しい主張(真である命題)です。
「 が より大きいならば, は より大きい」
の対偶は,
「 が 以下ならば, は 以下である」
※例2は,どちらも正しくない主張(偽である命題)です。例えば とすればわかります。
「数学ならば面白い」
の対偶は,
「面白くないなら数学ではない」
※例3のように,対偶という言葉は数学の世界の外(日常会話など)でも使います。
対偶の真偽は一致する
対偶の真偽は一致する
-
もとの命題と対偶の真偽は必ず一致します。
-
例えば,上の例1は両方とも真でした。例2は両方とも偽でした。
-
例えば,上の例3だと,数学が面白い人にとっては「数学ならば面白い」「面白くないなら数学ではない」どちらも真ですし,数学が面白くない人にとってはどちらも偽です。
-
対偶の真偽が一致することは,ベン図で理解することもできます。
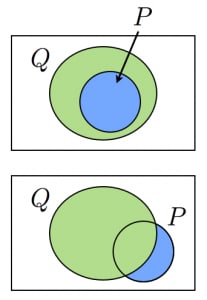 「 ならば 」が真
「 ならば 」が真
が に含まれている
の外側が の外側に含まれている
「 でないならば でない」が真 -
上側のベン図は, ならば およびその対偶が真である状況。下側のベン図はいずれも偽である状況を表しています。
対偶法
対偶法
対偶はもとの命題と真偽が一致しているので,もとの命題の証明をしたいときに代わりに対偶を証明してもOKというわけです。対偶を取ると証明しやすくなることもけっこうあります!
整数 に対して が奇数ならば も奇数であることを証明せよ。
対偶を取る。「 が偶数なら が偶数」を証明すればよい。 が偶数のとき は偶数3つの和なので偶数となりOK。
注: 命題の仮定部分が複雑だと証明しにくいことが多いです。「 が奇数」というやや複雑な仮定から逃げるために対偶を取って「 が偶数」という仮定にします。
いろいろな例題
いろいろな例題
を整数とする。不定方程式 が整数解を持つとき と が互いに素であることを証明せよ。
対偶を取る。 と が互いに素でないとき,不定方程式 が整数解を持たないことを証明すればよい。
実際, と がいずれも の倍数なら も の倍数となり, は整数解を持たない。
注:重要な定理の片側です。→一次不定方程式ax+by=cの整数解
最後はややマニアックです。興味のある人だけどうぞ!
なる自然数 が存在するとき, が合成数であることを証明せよ。
対偶を取る。 が素数のとき,全ての自然数 に対して を証明すればよい。これはフェルマーの小定理と呼ばれる有名な定理である!
注:例題3は が合成数であるための十分条件を与えてくれています。これを用いると与えられた整数が素数かどうか高確率で判定できます(フェルマーテスト)。
対偶を使った証明問題を集めたら,整数問題ばっかりになってしまいました。











