二次関数の最大値，最小値の2通りの求め方

$y=x^2-4x+5\\ =x^2-4x+4-4+5\\ =(x-2)^2+1$

よって，この二次関数の 頂点は $(2,1)$ であり，二次の係数が正なので下に凸である。

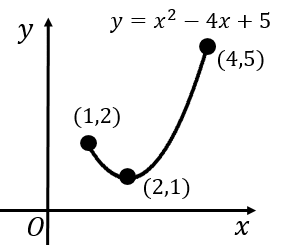
したがって，グラフは図のようになる。

よって，

最大値は $5$（$x=4$ のとき）

最小値は $1$（$x=2$ のとき）

$y=x^2-4x+5$ を微分すると，

$y'=2x-4$

したがって，$x=2$ がこの二次関数の軸となることが分かる。

また，グラフは $x=2$ に関して対称なので，区間の端の中で，$2$ からより遠い $x=4$ で最大値を取ることが分かる。

よって，

最大値は $5$ （$x=4$ のとき）

最小値は $1$ （$x=2$ のとき）

$y=-3x^2-4x+1\\ =-3\left(x^2+\dfrac{4}{3}x+\dfrac{4}{9}-\dfrac{4}{9}\right)+1\\ =-3\left(x+\dfrac{2}{3}\right)^2+\dfrac{7}{3}$

よって，この二次関数の頂点は $\left(-\dfrac{2}{3},\dfrac{7}{3}\right)$ であり，二次の係数が負なので上に凸である。

したがって，グラフは図のようになる。

よって，

最大値は $\dfrac{7}{3}$（$x=-\dfrac{2}{3}$ のとき）

最小値は存在しない

$y=-3x^2-4x+1$ を微分すると，

$y'=-6x-4$

したがって，$x=-\dfrac{2}{3}$ がこの二次関数の軸となることが分かる。

また，グラフは $x=-\dfrac{2}{3}$ に関して対称である。そして，区間の「端」の中で，$-\dfrac{2}{3}$ からより遠い側の端点は定義域に含まれない。

よって，

最大値は $\dfrac{7}{3}$（$x=-\dfrac{2}{3}$ のとき）

最小値は存在しない