無限等比級数の収束，発散の条件と証明など

$a,ar,ar^2,...$ は初項が $a$ で公比が $r$ の等比数列です。

この各項を足し合わせた無限和 $$a+ar+ar^2+\cdots$$ のことを無限等比級数と言います。

例えば，$1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}\cdots$ は $a=1,r=\dfrac{1}{2}$ である無限等比級数です。

冒頭で述べたように，公比 $r$ が $-1<r<1$ を満たすとき， $$a+ar+ar^2+\cdots=\dfrac{a}{1-r}$$ が成立します。

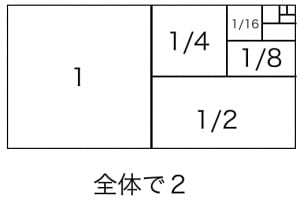
余談：図による説明

公式を知らなくても，例題1の級数が $2$ に収束することは下図を見れば納得できます。

以下，初項について $a\neq 0$ とします。

無限等比級数は $-1<r<1$ の場合は収束しますが，$|r|\geqq 1$ の場合は収束せず発散します。より詳しく言うと，

• $a > 0,r \geqq 1$ のとき正の無限大に発散（→例題2）
• $a <0,r \geqq 1$ のとき負の無限大に発散（→例題3）
• $r\leqq -1$ のとき振動（→例題4）

です。→数列の発散，収束，振動の意味と具体例

高校数学の問題集　～最短で得点力を上げるために～ のT160では，もう少しだけ難しい問題と，計算ミスを減らすコツを紹介しています。

では，以下の無限等比級数の公式を証明してみましょう。

等比数列の和の公式を知っていれば，極限を取るだけで簡単に証明できます。ただし，$r=1$ の場合は等比数列の和の形が異なるので場合分けが必要です。

• $a+ar+ar^2+\cdots$ をシグマを使って表すと，
  $$a+ar+ar^2+\cdots=\displaystyle\sum_{k=1}^{\infty}ar^{k-1}$$ となります。

• 等比数列の和の公式 $\dfrac{a(r^n-1)}{r-1}$ よりも無限等比級数の公式 $\dfrac{a}{1-r}$ の方が綺麗です。これは，極限を取る操作のおかげで $ar^n$ の項が消えるためです。

• 「無限級数」という言葉は「無限項の和」を表します。「無限級数の和」という言葉にはやや違和感を感じます（頭痛が痛いみたいな感じ）。

• $\dfrac{a}{1-r}$ に収束する場合について，以下が成立するのは直感的にも納得できます。
  

  • 無限等比級数の値が初項 $a$ に比例する
  • 公比 $r$ が $1$ に近いほど（絶対値が）大きくなり $r\to 1$ で発散する

Tag:数列の和を計算するための公式まとめ

Tag:数学3の教科書に載っている公式の解説一覧