平面グラフ・平面的グラフの意味とオイラーの定理の応用

• グラフとは，点の集合 $V$ と二点間を結ぶ辺の集合 $E$ のペアです。
  →グラフ理論の基礎

• 例えば，下図は，4つの頂点とすべての2点間を結んだ「完全グラフ $K_4$」です。

• 平面グラフ(Plane Graph)とは，平面に「辺の交差なし」で描かれたグラフのことです。例えば，さきほどの $K_4$ は真ん中に交差点があるので平面グラフではありません。しかし，下図のように（点どうしのつなぎ方を変えないように）描き方を変えれば平面グラフになります。

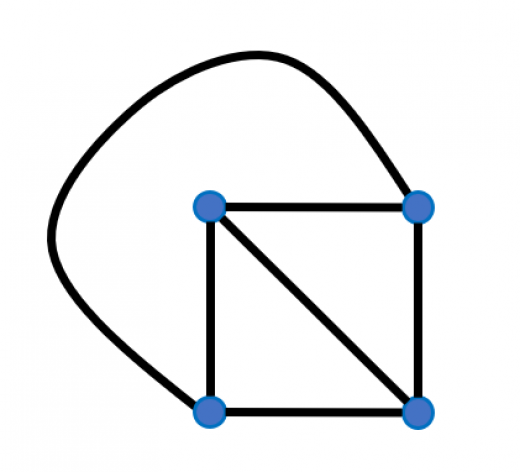
• 平面的グラフ(Planar Graph)とは，頂点以外の点で辺が交差しないように平面に描けるようなグラフです。$K_4$ は平面的グラフです（平面的グラフを実際に交差なしで描いたものが平面グラフです）。

なお，グラフ理論では平面に「描く」と言わずに 「埋め込む」と言うので，以下でも「埋め込む」という言葉を使います。

この記事の目標は $K_5$，$K_{3,3}$ が平面的グラフでないことを証明することです。$K_5$ や $K_{3,3}$ はどう頑張っても平面に交差なしで埋め込めないのです！

$K_5$ や $K_{3,3}$ が平面的グラフでないことを証明するためにオイラーの定理を用います。

例えば，さきほどの $K_4$ の例（右上図）では $v=4,e=6,f=4$ となりオイラーの定理が成立しています。

証明は，空間図形（凸多面体）におけるオイラーの多面体定理と同様です。オイラーの多面体定理の意味と証明のstep2以降を参照して下さい。

補足： $$2e=\displaystyle\sum_{F_0\in F}e(F_0)\geq\displaystyle\sum_{F_0\in F}3=3f$$

ただし，$F$ は面全体の集合，$e(F_0)$ は $F_0$ に隣接する辺の数です。

大筋はさきほどと同じですが，$K_{3,3}$ の場合には $e\leq 3v-6$ ではうまくいきません。二部グラフであることを使ってより強い不等式を導きます。

最後に，非常に発展的ですがクラトフスキーの定理を紹介しておきます。与えられたグラフが平面的グラフかどうか判定するために使える偉大な定理です。

• 「マイナーとして」という部分は厳密に説明するのはやや大変です，気になる人は調べてみてください。
• $K_5$ や $K_{3,3}$ は平面的グラフではないということから $\Rightarrow$ は上記の議論でなんとなく納得できるでしょう。
• $\Leftarrow$ がすごい結果です。証明はかなり難しいです。