グラフ理論の基礎

• グラフとは，点の集合 $V$ と二点間を結ぶ辺の集合 $E$ のペアです。
• $G=(V,E)$ などと表します。
• 点のことを頂点，ノード(vertex,node)，辺のことを枝(arc,edge)などと呼びます。
• グラフは組み合わせ的な構造を表すモデルです。そのため，図における二つのグラフは同じとみなします。 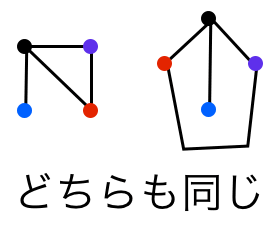頂点の置き方やどのような曲線で結ばれているかは考えません（図では分かりやすくするために頂点に色をつけています）。
• 辺に方向性があるようなグラフを有向グラフ，方向性がないようなものを無向グラフと呼びます。図は無向グラフです，有向グラフでは辺を矢印で表します。問題によって使い分けましょう。

感覚的にはごく自然な用語たちです。いろいろな概念を簡潔に表現することができるので便利です。

• （頂点の）次数：頂点から出ている辺の本数。
• 連結：どの頂点からどの頂点へも辺を伝っていくことができるようなグラフ。
• パス（道）：隣接する頂点をたどったもの。ただし，「同じ頂点を二回通るのはダメ」とすることが多い。
• サイクル（閉路）：隣接する頂点をたどったもので，始点と終点が同じもの。ただし，同じ辺を二回通るのはダメ。

• 木：閉路が存在しない連結なグラフ。
• 単純グラフ：多重辺や自己ループを含まないグラフ。
• 二部グラフ：頂点が二つのグループに分かれており，異なるグループの頂点間にのみ辺が引かれているグラフ。
• 完全グラフ：全ての頂点間に辺が引かれているグラフ。頂点数 $n$ の完全グラフを $K_n$ と書く（図は $K_5$）。
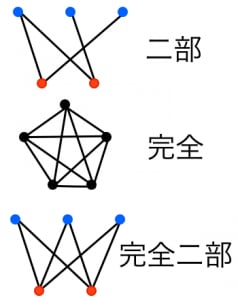
• 完全二部グラフ：二部グラフで，異なるグループの頂点間には全て辺が引かれているグラフ。グループの頂点数がそれぞれ $m,n$ である完全二部グラフを $K_{m,n}$ と書く（図は $K_{3,2}$）。
• オイラーグラフ：一筆書きできるグラフ。→オイラーグラフの定理（一筆書きできる条件）とその証明

他にも，ピーターセングラフ，パーフェクトグラフなどもあります。

数学オリンピックではグラフ理論を使うとスッキリと記述できる問題が多く出題されています。このような問題はグラフ理論を全く知らなくても解けるようになっており．グラフ理論の難しい定理を知っていて有利になる場面は少ないです。

しかし，グラフ理論を知っていると問題を簡潔に記述でき，見通しがよくなります。「人間」とか「知り合い」などの日本語で議論するよりもグラフを描いて頂点と辺で議論した方が圧倒的に分かりやすいです。

そのような意味で，最低限のグラフ理論の概念と用語を知っていると数学オリンピックでは有利です。

例

• 2001JMO本選問1：握手の補題とエルデシュガライの定理
• 2014JJMO本選問4：2014年JJMO本選第4問の解説
• 1992IMO問3：ラムゼーの定理と6人の問題

他にもいくらでもあります！