2014年JJMO本選第4問の解説
組み合わせの良問を紹介します。証明だけでなく，考え方や重要なテクニックも紹介します。
グラフ理論の言葉を使わないので問題文が少し長いですが，意味は単純です。
を 以上の整数とする。大きさの異なる 個の島があり，その島を繋ぐいくつかの橋がある。どの つの島も 本の橋で結ばれているかいないかのいずれかであって，橋の両端は相異なる つの島につながっている。
さて，これらの島はそれぞれの避難先を求めて災害に備えることにした。各々の島では，橋でその島と直接結ばれている島が1つ以上あったのでこのうち最も大きい島を避難先にした。
（1） が奇数ならば，どの島の避難先ともならない島が存在することを示せ。
（2） が偶数であり橋が 本より多く存在するならば，どの島の避難先ともならない島が存在することを示せ。
グラフ理論の言葉を使うと「孤立点のない単純グラフ」を考える，ということです。
証明の方針
（1）の証明
（2）の証明
証明の方針
(1),(2)ともに，「ある条件を満たす」→「どの島の避難先ともならない島が存在する」という形の命題で扱いにくいので，
「どの島の避難先ともならない島は存在しない」→「ある条件は満たされない」
を証明します（対偶法）。
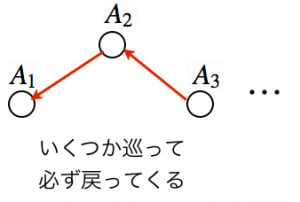
そして「どの島も，とある島から避難先に指定されている」ことを利用してサイクルを作ります：
適当に島 を選ぶ。 を避難先とする島 が存在する。さらに を避難先とする島 が存在する。これを繰り返していくといつか に戻ってくる（避難先は1つしかないので など途中の島に戻ってくることはない）。このかたまりをサイクルと呼ぶことにする。
上記が核心部分です。サイクルを作ることに気づけば（1）は解けたようなものです。（2）ではもう一工夫必要になります。
ちなみに， このようにグラフをたどっていきサイクルを作り出す議論は，数学オリンピックの問題や大学で学ぶグラフ理論で頻出です。
（1）の証明
より が大きいことを と書くことにします。
上記の議論により，島たちはいくつかのサイクルに分解できる（全ての島はどれか1つのサイクルに属する）。よって，島の数 が奇数のサイクルがないことを示せば良い。
これは例えば で実験すれば簡単に分かる：
の避難先が なので
の避難先が なので
以下同様に， となる。
しかし， つの不等式より となるので矛盾。
一般の奇数の場合も全く同様に証明できる。
以上から，「どの島もとある島から避難先に指定されている」ならばいくつかの偶サイクルで表せることが分かったので（1）が示された。
（2）の証明
実は，ほぼ同様な手法で が 以上の偶数でもダメだということが分かります。
つまり， が 以上の偶数の場合：
となり矛盾。
ここに気づくのが（2）の山になります。
よって， のみとなります。つまり，島たちはいくつかのペアに分解できます！
個の島は 個のペアに分解できた。あとは異なるペアの間にかかる橋を数えればよい。
異なるペア とペア の間にかかる橋は多くても2本（※）なので，全体の橋の数は最大で，
（※）「避難先の関係を保ったまま異なるペアに2本橋をかけることができる」のは図から分かります。
「避難先の関係を保ったまま異なるペアに3本以上橋をかけることはできない」のは4つの島の大小関係を場合分けしてしらみつぶしに調べれば確かめられます。
グラフ理論に少しでもなじみがあると取っ付きやすい問題でした。 →グラフ理論の基礎
JJMO(日本ジュニア数学オリンピック)の組み合わせの問題はJMOの対策にもなりますね。
Tag:各地の数オリの過去問