オイラーの多面体定理の意味と証明
任意の(穴のない)多面体について,
が成立する。ただし,頂点の数を , 辺の数を , 面の数を とした。

例
例
オイラーの多面体定理は非常に美しい定理です。まずは簡単な例で確認してみます。
四面体では, より,

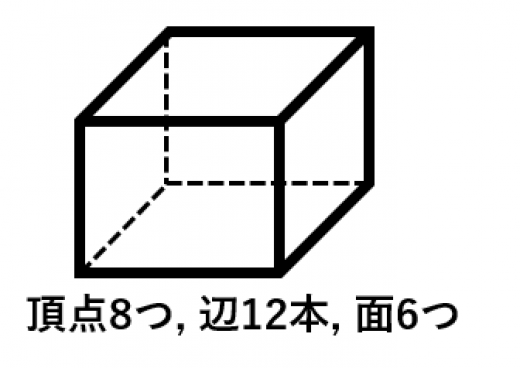
六面体(サイコロ,立方体,直方体)では, より,
正八面体,正12面体,正20面体について, であることを確認してみよう。
覚え方
覚え方
オイラーの多面体定理: について,
-
記号は,それぞれの単語:頂点(Vertex), 辺(Edge), 面(Face)の英単語の頭文字に由来しています。3つの英単語を覚えれば記号は混同しなくなるでしょう。
-
あとは,2つ足して1つ引くということはなかなか忘れないですが,どの2つを足すのか忘れやすいので,そのときには 四面体で確認するとよいでしょう。
オイラーの多面体定理の証明
オイラーの多面体定理の証明
オイラーの多面体定理を4段階に分けて証明します。1つ1つは難しくないですが,4つ組み合わせると美しい定理の証明ができてしまいます。図は立方体の例です。

Step1: 多面体を平面グラフに展開(ちょいむず)
Step2: 平面グラフを三角形に分割(かんたん)
Step3: 三角形を除いていく(ふつう)
Step4: 最後に三角形で確認(かんたん)
Step1:多面体を平面グラフに展開
 3次元だと考えにくいので,2次元に展開して考えます。イメージとしては,
「多面体の面を1つ選んで,その面を取り除き,その穴から手を突っ込んで押し広げながら潰す」感じです。このとき,頂点や辺の数は変わらず,面を1つ取り除くので,展開された平面図形において,
を示せばよいわけです。立方体の図の例では,青い辺で囲まれた面を取り除いて展開しています。
3次元だと考えにくいので,2次元に展開して考えます。イメージとしては,
「多面体の面を1つ選んで,その面を取り除き,その穴から手を突っ込んで押し広げながら潰す」感じです。このとき,頂点や辺の数は変わらず,面を1つ取り除くので,展開された平面図形において,
を示せばよいわけです。立方体の図の例では,青い辺で囲まれた面を取り除いて展開しています。
Step2:平面グラフを三角形に分割

得られた平面図形には様々な多角形が含まれており,統一的に議論したいので三角形に直します。三角形でない図形は適当に対角線を引いて三角形に分割します。対角線を引くときに,面と辺の数が1つずつ増えるので の値は変わりません。
よって,分割後の図形で を示せばよいわけです。
Step3:三角形を除いていく
得られた図形の の値を保ったまま外側の三角形から順々に消していきます。
操作1:外側と1辺を共有する三角形を除くと辺と面が1つずつ減るので, は変わりません。
操作2:外側と2辺を共有する三角形を除くと頂点と面が1つずつ減り辺が2つ減るので, は変わりません。
三角形の数は有限なので, この操作を繰り返し行うといつかは三角形1つになります。(厳密には操作の途中で図形が分断されるのを防ぐため,操作2を操作1より優先して行う必要があります)

Step4:最後に三角形で確認
三角形では,頂点3,辺3,面1より, が成立します。
以上からオイラーの多面体定理が証明されました!
ちなみに,球面上の多角形の面積公式を用いた別証も美しいのでおすすめです。→球面上の多角形の面積と美しい応用
昔はとても大好きな定理だったのですが,見慣れてしまったせいか,最近は「そこそこ好きな定理」になりました。
Tag:オイラーの公式・定理まとめ
Tag:とにかく美しい数学公式まとめ











