図形と図形で”はさみうち”~京大特色2025第3問
座標平面における領域 で定まる図形 を考える。 に対して,原点を中心とする回転や平行移動を,何回か行って得られる図形を 個用意し,それぞれ とする。
このとき, により座標平面を覆うことのできる の最小値を求めよ。
この記事では京大特色入試の問題を解説します。シンプルで深い知識は必要ないものの,テクニックが問われる良問です。
解答の指針
解答の指針
最小値を求める問題は
- 最小値で実際に解が構成できることを確認する
- それ未満で不可能であることを示す
という2ステップで議論することがポイントです。
解答
解答
ステップ1:例の構成
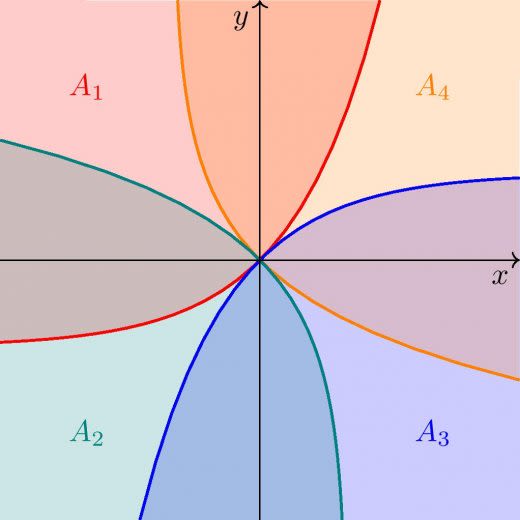
まず4個で覆うことができることを確認する。
とおく。これは を平行移動したものである。また, は第2象限をすべて含む。
を ,, 回転させたものを順に とすると,順に第3,4,1象限を含むため,これらで座標平面を覆うことができる。
ステップ1を元にした考察
ステップ1で構成した例のポイントは, が座標平面を四等分したときの1パーツ()を含んでいることです。
3つで覆えるかどうか考察するため,座標平面を3等分したときの1パーツと を比較してみましょう。
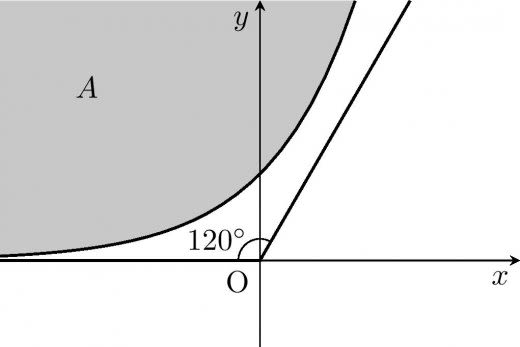
のほうが含まれます。
を含み3等分したパーツに含まれる,より小さい「扇」を用意して,その図形3つでは座標平面を覆えないことを示せば, 3つで座標平面を覆えないことも分かります。
ステップ2:それ未満の解がないこと
以下の議論を簡単にするため,1点(頂点と呼ぶ)とその点を端とする半直線2本で囲まれる図形を扇ということにする。扇は線対称な図形であることに注意したい。
※ ベクトルを用いると次のように表すことができる図形を指す。
以下,()というマークが付いている箇所は図より従うということで証明をしていません。実際に証明を書く場合は,上で定義した扇のベクトルによる表示によって確認することができます。
を含む扇を作る。
原点を通り と接する直線は である。よって とすると である。
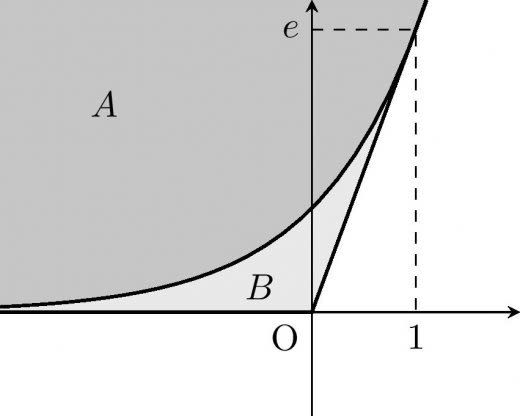
よって以下 に対して,原点を中心とする回転や平行移動を,何回か行って得られる図形3つで座標平面を覆えると仮定して矛盾を示す。( で覆えないのであれば, の部分集合である でも覆うことはできないためこれで題意が示される。)
以下議論のために図のように
- 扇 の頂点(点 )を
- 半直線 を
- 半直線 を
とおく。
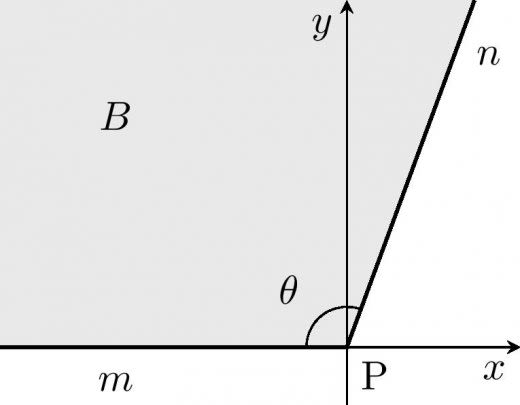
で対応する図形を順に ,, とおく。 の図形を境界と呼ぶ。
また, の頂角( と で挟まれる角のうち小さい方)の大きさを とおく。 より である。
適切に回転と平行移動をすることで としてよい。
また,議論のために直線 を新たに 軸とよぶことにする。
さらに である場合を考える。 をその線対称の軸に沿って を含むように平行移動したものを とおくと, であるため, を に取り換えて議論してよい。ゆえに はどれも を含むものとして議論する。
加えて または に沿った平行移動を行うことで, について のうち片方だけが と共通部分を持つとしてよい。
- と が共通部分を持つ場合
の傾きをそれぞれ とおく。
は を 回転させた図形と共通部分を持つ。 を 方向に平行移動させても共通部分を持つため,原点を通りそれぞれと平行な直線を考えることで を得る。
は の負方向に延びる半直線である()であるため,十分大きい正の実数 について は に含まれない。
また, の傾きは であるため, は にも含まれない。
よってこれは矛盾する。
- と が共通部分を持つ場合
上のケースと同様に考える。 の傾きをそれぞれ とおくと である。
なお,不等式の左は を満たす を取ると, の加法定理より と得られる。
よって十分大きい について とおくとこれはどの にも含まれない。よって矛盾が生じる。
- と が共通部分を持つ場合
の傾きを とすると,1つ目のケースと同様に考えることで となる。
の傾きを とすると,2つ目のケースと同様に考えることで となる。
さて より である。
ゆえに原点から十分遠い箇所で は常に よりも反時計回りに進んだ位置にある。つまり を満たす実数を取ると,十分大きな正の実数 について は どちらにも含まれない。
また, であるため, にも含まれない。
こうした点の存在は では座標平面を覆うことと矛盾する。
よって に対して,原点を中心とする回転や平行移動を,何回か行って得られる図形3つで座標平面を覆うことはできない。 より についても同様に原点を中心とする回転や平行移動を,何回か行って得られる図形3つで座標平面を覆うことはできない。
こうして求める の最小値は である。
扱いやすい配置に帰着させて具体的な式で攻めることがポイントでした。非常に良い問題ですね。











