解答例
星の名前の定義
帰納的に,f : X → Y f:X \to Y f : X → Y S f S_f S f X Y XY X Y
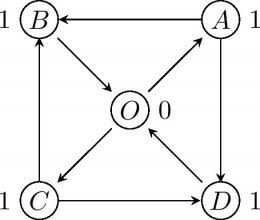
このとき,星 X X X X X X O O O
星と航路の対応
次に n n n
(a) :星 X X X n n n n + 1 n+1 n + 1 X 0 → X 1 → ⋯ → X n X_0 \to X_1 \to \cdots \to X_n X 0 → X 1 → ⋯ → X n
(b) :星 X X X Y Y Y X 1 = Y 0 , ⋯ , X n = Y n − 1 X_1 = Y_0 , \cdots , X_n = Y_{n-1} X 1 = Y 0 , ⋯ , X n = Y n − 1
n = 1 n=1 n = 1
n = k n=k n = k k k k X X X Y Y Y X Y XY X Y X 0 → X 1 → ⋯ → X k → Y k X_0 \to X_1 \to \cdots \to X_k \to Y_k X 0 → X 1 → ⋯ → X k → Y k
X Y XY X Y X Y XY X Y Y Y Y f ′ f' f ′ S f ′ S_{f'} S f ′
直行便 f ′ : Y → Z f' : Y \to Z f ′ : Y → Z Y 2 = Z 1 , ⋯ , Y k = Z k − 1 Y_2 = Z_1 , \cdots , Y_k = Z_{k-1} Y 2 = Z 1 , ⋯ , Y k = Z k − 1 X Y → Y Z XY \to YZ X Y → Y Z X 0 → X 1 → ⋯ → X k → Y k → Z k X_0 \to X_1 \to \cdots \to X_k \to Y_k \to Z_k X 0 → X 1 → ⋯ → X k → Y k → Z k
よって成立する。
経路から星の名前を定める
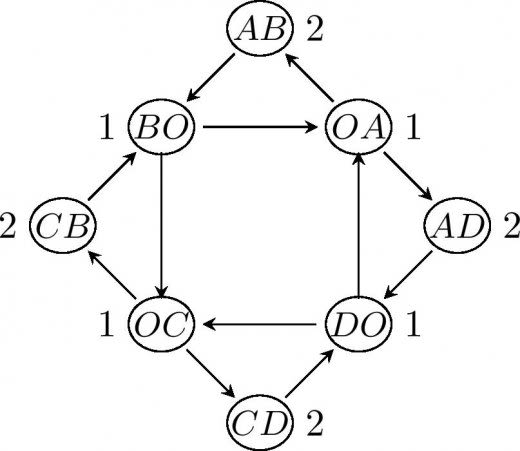
経路 X 0 → X 1 → ⋯ → X n X_0 \to X_1 \to \cdots \to X_n X 0 → X 1 → ⋯ → X n X m ( m = 0 , 1 , ⋯ , n ) X_m \ (m = 0,1, \cdots , n) X m ( m = 0 , 1 , ⋯ , n ) X ( m ) X(m) X ( m ) X ( k ) = n C k X(k) = {}_n \mathrm{C}_k X ( k ) = n C k
n n n n = 1 n=1 n = 1
n = k n=k n = k X → Y X \to Y X → Y X Y XY X Y m = 0 , k + 1 m=0,k+1 m = 0 , k + 1 X Y ( 0 ) = X ( 0 ) = 1 , X Y ( k + 1 ) = Y ( k ) = 1 XY(0) = X(0) = 1, XY(k+1) = Y(k) = 1 X Y ( 0 ) = X ( 0 ) = 1 , X Y ( k + 1 ) = Y ( k ) = 1
m = 1 , 2 , ⋯ , k m =1,2, \cdots , k m = 1 , 2 , ⋯ , k ( X Y ) m = X m = Y m + 1 (XY)_m = X_m = Y_{m+1} ( X Y ) m = X m = Y m + 1 X Y ( m ) = X ( m ) + Y ( m + 1 ) XY(m) = X(m) + Y(m+1) X Y ( m ) = X ( m ) + Y ( m + 1 )
帰納法の仮定から X ( m ) = k C m X(m) = {}_k \mathrm{C}_m X ( m ) = k C m Y ( m + 1 ) = k C m + 1 Y(m+1) = {}_k \mathrm{C}_{m+1} Y ( m + 1 ) = k C m + 1 X Y ( m ) = k + 1 C m XY(m) = {}_{k+1} \mathrm{C}_m X Y ( m ) = k + 1 C m
経路の場合分け
元のグラフから,どのような経路においても3回に1度 O O O O O O
航路の対称性から,まずは O , A , B O,A,B O , A , B A A A B B B C C C D D D
出発点が O O O
経路は
O A B O A B ⋯ O A B undefined 33 セット O A
\underbrace{OABOAB \cdots OAB}_{33\ \text{セット}} OA
33 セット O A BO A B ⋯ O A B O A
この経路に対応する星の重要度は
0 ⋅ 100 C 0 + 1 ⋅ 100 C 1 + 1 ⋅ 100 C 2 + ⋯ + 0 ⋅ 100 C 99 + 1 ⋅ 100 C 100
0 \cdot {}_{100} \mathrm{C}_0 + 1 \cdot {}_{100} \mathrm{C}_1 + 1 \cdot {}_{100} \mathrm{C}_2 + \cdots + 0 \cdot {}_{100} \mathrm{C}_{99} + 1 \cdot {}_{100} \mathrm{C}_{100}
0 ⋅ 100 C 0 + 1 ⋅ 100 C 1 + 1 ⋅ 100 C 2 + ⋯ + 0 ⋅ 100 C 99 + 1 ⋅ 100 C 100
同様に O O O A A A B B B 33 33 33 2 67 2^{67} 2 67
1回目の移動で初めて O O O
O , A , B O,A,B O , A , B B O A B O A ⋯ B O A undefined 33 セット B O
\underbrace{BOABOA \cdots BOA}_{33\ \text{セット}} BO
33 セット BO A BO A ⋯ BO A BO
この経路に対応する星の重要度は
1 ⋅ 100 C 0 + 0 ⋅ 100 C 1 + 1 ⋅ 100 C 2 + ⋯ + 1 ⋅ 100 C 99 + 0 ⋅ 100 C 100
1 \cdot {}_{100} \mathrm{C}_0 + 0 \cdot {}_{100} \mathrm{C}_1 + 1 \cdot {}_{100} \mathrm{C}_2 + \cdots + 1 \cdot {}_{100} \mathrm{C}_{99} + 0 \cdot {}_{100} \mathrm{C}_{100}
1 ⋅ 100 C 0 + 0 ⋅ 100 C 1 + 1 ⋅ 100 C 2 + ⋯ + 1 ⋅ 100 C 99 + 0 ⋅ 100 C 100
同様の経路は,上の経路において A A A B B B 34 34 34 2 67 2^{67} 2 67
2回目の移動で初めて O O O
O , A , B O,A,B O , A , B A B O A B O ⋯ A B O undefined 33 セット A B
\underbrace{ABOABO \cdots ABO}_{33\ \text{セット}} AB
33 セット A BO A BO ⋯ A BO A B
この経路に対応する星の重要度は
1 ⋅ 100 C 0 + 1 ⋅ 100 C 1 + 0 ⋅ 100 C 2 + ⋯ + 1 ⋅ 100 C 99 + 1 ⋅ 100 C 100
1 \cdot {}_{100} \mathrm{C}_0 + 1 \cdot {}_{100} \mathrm{C}_1 + 0 \cdot {}_{100} \mathrm{C}_2 + \cdots + 1 \cdot {}_{100} \mathrm{C}_{99} + 1 \cdot {}_{100} \mathrm{C}_{100}
1 ⋅ 100 C 0 + 1 ⋅ 100 C 1 + 0 ⋅ 100 C 2 + ⋯ + 1 ⋅ 100 C 99 + 1 ⋅ 100 C 100
同様の経路は,上の経路において A A A B B B 34 34 34 2 68 2^{68} 2 68
重要度の総和
上記の計算により重要度の総和は
( 0 ⋅ 100 C 0 + 1 ⋅ 100 C 1 + 1 ⋅ 100 C 2 + ⋯ + 0 ⋅ 100 C 99 + 1 ⋅ 100 C 100 ) × 2 67 + ( 1 ⋅ 100 C 0 + 0 ⋅ 100 C 1 + 1 ⋅ 100 C 2 + ⋯ + 1 ⋅ 100 C 99 + 1 ⋅ 100 C 100 ) × 2 67 + ( 1 ⋅ 100 C 0 + 1 ⋅ 100 C 1 + 0 ⋅ 100 C 2 + ⋯ + 1 ⋅ 100 C 99 + 0 ⋅ 100 C 100 ) × 2 68 = ( 1 ⋅ 100 C 0 + 1 ⋅ 100 C 1 + 1 ⋅ 100 C 2 + ⋯ + 1 ⋅ 100 C 99 + 1 ⋅ 100 C 100 ) × 3 × 2 67 − ( 100 C 2 + 100 C 5 + ⋯ + 100 C 98 ) × 2 67 = 3 × 2 67 × 2 100 − ( 100 C 2 + 100 C 5 + ⋯ + 100 C 98 ) × 2 67 \begin{aligned}
& (0 \cdot {}_{100} \mathrm{C}_0 + 1 \cdot {}_{100} \mathrm{C}_1 + 1 \cdot {}_{100} \mathrm{C}_2 +\\
& \quad \cdots + 0 \cdot {}_{100} \mathrm{C}_{99} + 1 \cdot {}_{100} \mathrm{C}_{100}) \times 2^{67}\\
+& (1 \cdot {}_{100} \mathrm{C}_0 + 0 \cdot {}_{100} \mathrm{C}_1 + 1 \cdot {}_{100} \mathrm{C}_2 +\\
&\quad \cdots + 1 \cdot {}_{100} \mathrm{C}_{99} + 1 \cdot {}_{100} \mathrm{C}_{100}) \times 2^{67}\\
+& (1 \cdot {}_{100} \mathrm{C}_0 + 1 \cdot {}_{100} \mathrm{C}_1 + 0 \cdot {}_{100} \mathrm{C}_2 +\\
& \quad \cdots + 1 \cdot {}_{100} \mathrm{C}_{99} + 0 \cdot {}_{100} \mathrm{C}_{100}) \times 2^{68}\\
=& (1 \cdot {}_{100} \mathrm{C}_0 + 1 \cdot {}_{100} \mathrm{C}_1 + 1 \cdot {}_{100} \mathrm{C}_2 +\\
& \cdots + 1 \cdot {}_{100} \mathrm{C}_{99} + 1 \cdot {}_{100} \mathrm{C}_{100}) \times 3 \times 2^{67}\\
& - ({}_{100} \mathrm{C}_2 + {}_{100} \mathrm{C}_{5} + \cdots + {}_{100} \mathrm{C}_{98}) \times 2^{67}\\
=& \ 3 \times 2^{67} \times 2^{100} - ({}_{100} \mathrm{C}_2 + {}_{100} \mathrm{C}_{5} + \cdots + {}_{100} \mathrm{C}_{98}) \times 2^{67}
\end{aligned} + + = = ( 0 ⋅ 100 C 0 + 1 ⋅ 100 C 1 + 1 ⋅ 100 C 2 + ⋯ + 0 ⋅ 100 C 99 + 1 ⋅ 100 C 100 ) × 2 67 ( 1 ⋅ 100 C 0 + 0 ⋅ 100 C 1 + 1 ⋅ 100 C 2 + ⋯ + 1 ⋅ 100 C 99 + 1 ⋅ 100 C 100 ) × 2 67 ( 1 ⋅ 100 C 0 + 1 ⋅ 100 C 1 + 0 ⋅ 100 C 2 + ⋯ + 1 ⋅ 100 C 99 + 0 ⋅ 100 C 100 ) × 2 68 ( 1 ⋅ 100 C 0 + 1 ⋅ 100 C 1 + 1 ⋅ 100 C 2 + ⋯ + 1 ⋅ 100 C 99 + 1 ⋅ 100 C 100 ) × 3 × 2 67 − ( 100 C 2 + 100 C 5 + ⋯ + 100 C 98 ) × 2 67 3 × 2 67 × 2 100 − ( 100 C 2 + 100 C 5 + ⋯ + 100 C 98 ) × 2 67
最後の項を計算する。ただし ω = − 1 + 3 i 2 \omega = \dfrac{-1+\sqrt{3}i}{2} ω = 2 − 1 + 3 i ω 3 = 1 \omega^3 = 1 ω 3 = 1 ( 100 C 2 + 100 C 5 + ⋯ + 100 C 98 ) × 3 = ( 100 C 0 + 100 C 3 + ⋯ + 100 C 99 ) × ( ω 2 + ω + 1 ) + ( 100 C 1 + 100 C 4 + ⋯ + 100 C 100 ) × ( ω 2 + ω + 1 ) + ( 100 C 2 + 100 C 5 + ⋯ + 100 C 98 ) × 3 = ( 100 C 0 + 100 C 1 + ⋯ + 100 C 100 ) + ( 100 C 0 ω 0 + 100 C 1 ω 1 + ⋯ + 100 C 100 ω 100 ) × ω + ( 100 C 0 ω 0 + 100 C 1 ω 2 + ⋯ + 100 C 100 ω 200 ) × ω 2 = ( 1 + 1 ) 100 + ω ( 1 + ω ) 100 + ω 2 ( 1 + ω 2 ) 100 \begin{aligned}
&({}_{100} \mathrm{C}_2 + {}_{100} \mathrm{C}_{5} + \cdots + {}_{100} \mathrm{C}_{98}) \times 3 \\
&= ({}_{100} \mathrm{C}_0 + {}_{100} \mathrm{C}_{3} + \cdots + {}_{100} \mathrm{C}_{99}) \times (\omega^2 + \omega + 1)\\
&\quad + ({}_{100} \mathrm{C}_1 + {}_{100} \mathrm{C}_{4} + \cdots + {}_{100} \mathrm{C}_{100}) \times (\omega^2 + \omega + 1)\\
&\quad + ({}_{100} \mathrm{C}_2 + {}_{100} \mathrm{C}_{5} + \cdots + {}_{100} \mathrm{C}_{98}) \times 3\\
&= ({}_{100} \mathrm{C}_0 + {}_{100} \mathrm{C}_{1} + \cdots + {}_{100} \mathrm{C}_{100})\\
&\quad + ({}_{100} \mathrm{C}_0 \omega^0 + {}_{100} \mathrm{C}_{1} \omega^1 + \cdots + {}_{100} \mathrm{C}_{100} \omega^{100}) \times \omega \\
&\quad + ({}_{100} \mathrm{C}_0 \omega^0 + {}_{100} \mathrm{C}_{1} \omega^2 + \cdots + {}_{100} \mathrm{C}_{100} \omega^{200}) \times \omega^2 \\
&= (1+1)^{100} + \omega (1+\omega)^{100} + \omega^2 (1+\omega^2)^{100}
\end{aligned} ( 100 C 2 + 100 C 5 + ⋯ + 100 C 98 ) × 3 = ( 100 C 0 + 100 C 3 + ⋯ + 100 C 99 ) × ( ω 2 + ω + 1 ) + ( 100 C 1 + 100 C 4 + ⋯ + 100 C 100 ) × ( ω 2 + ω + 1 ) + ( 100 C 2 + 100 C 5 + ⋯ + 100 C 98 ) × 3 = ( 100 C 0 + 100 C 1 + ⋯ + 100 C 100 ) + ( 100 C 0 ω 0 + 100 C 1 ω 1 + ⋯ + 100 C 100 ω 100 ) × ω + ( 100 C 0 ω 0 + 100 C 1 ω 2 + ⋯ + 100 C 100 ω 200 ) × ω 2 = ( 1 + 1 ) 100 + ω ( 1 + ω ) 100 + ω 2 ( 1 + ω 2 ) 100 ω + 1 = 1 + 3 i 2 = cos π 3 + i sin π 3 ω 2 + 1 = 1 − 3 i 2 = cos π 3 + i sin 5 π 3
\omega + 1 = \dfrac{1+\sqrt{3}i}{2} = \cos \dfrac{\pi}{3} + i \sin \dfrac{\pi}{3}\\
\omega^2 + 1 = \dfrac{1-\sqrt{3}i}{2} = \cos \dfrac{\pi}{3} + i \sin \dfrac{5\pi}{3}
ω + 1 = 2 1 + 3 i = cos 3 π + i sin 3 π ω 2 + 1 = 2 1 − 3 i = cos 3 π + i sin 3 5 π ( 1 + 1 ) 100 + ω ( 1 + ω ) 100 + ω 2 ( 1 + ω 2 ) 100 = 2 100 + ω ( cos 100 3 π + i sin 100 3 π ) + ω 2 ( cos 200 3 π + i sin 200 3 π ) = 2 100 + ω ( cos 4 3 π + i sin 4 3 π ) + ω 2 ( cos 2 3 π + i sin 2 3 π ) = 2 100 + 2 \begin{aligned}
&(1+1)^{100} + \omega (1+\omega)^{100} + \omega^2 (1+\omega^2)^{100}\\
&= 2^{100} + \omega \left( \cos \dfrac{100}{3} \pi + i \sin \dfrac{100}{3} \pi \right)\\
&\qquad \qquad + \omega^2 \left( \cos \dfrac{200}{3} \pi + i \sin \dfrac{200}{3} \pi \right)\\
&= 2^{100} + \omega \left( \cos \dfrac{4}{3} \pi + i \sin \dfrac{4}{3} \pi \right)\\
&\qquad \qquad + \omega^2 \left( \cos \dfrac{2}{3} \pi + i \sin \dfrac{2}{3} \pi \right)\\
&= 2^{100}+2
\end{aligned} ( 1 + 1 ) 100 + ω ( 1 + ω ) 100 + ω 2 ( 1 + ω 2 ) 100 = 2 100 + ω ( cos 3 100 π + i sin 3 100 π ) + ω 2 ( cos 3 200 π + i sin 3 200 π ) = 2 100 + ω ( cos 3 4 π + i sin 3 4 π ) + ω 2 ( cos 3 2 π + i sin 3 2 π ) = 2 100 + 2
よって,重要度の総和は
3 × 2 67 × 2 100 − 2 100 + 2 3 × 2 67 = 2 67 × 9 × 2 100 − 2 100 − 2 3 = 2 67 × 8 × 2 100 − 2 3 = 2 68 ( 2 102 − 1 ) 3 \begin{aligned}
&3 \times 2^{67} \times 2^{100} - \dfrac{2^{100}+2}{3} \times 2^{67}\\
&= 2^{67} \times \dfrac{9 \times 2^{100}-2^{100}-2}{3}\\
&= 2^{67} \times \dfrac{8 \times 2^{100}-2}{3}\\
&= \dfrac{2^{68} (2^{102}-1)}{3}
\end{aligned} 3 × 2 67 × 2 100 − 3 2 100 + 2 × 2 67 = 2 67 × 3 9 × 2 100 − 2 100 − 2 = 2 67 × 3 8 × 2 100 − 2 = 3 2 68 ( 2 102 − 1 )
 となります。
となります。 となります。
となります。











