鳩ノ巣原理の意味と例（身近な例から超難問まで）

$a,b,c,d$ を $3$ で割った余りに注目して $3$ グループに分けると，鳩ノ巣原理より，とある同じグループに $2$ 個以上属する。その $2$ 個は $3$ で割った余りが同じなので差が $3$ の倍数になる。

5つの格子点を，$x$ 座標，$y$ 座標がそれぞれ奇数か偶数かで4グループに分ける。

つまり，(奇，奇)，(奇，偶)，(偶，奇)，(偶，偶)　の4グループ。

すると，鳩ノ巣原理より同じグループに属する2点が存在する。偶奇が等しい整数の平均は整数なので，その2点の中点は格子点となる。

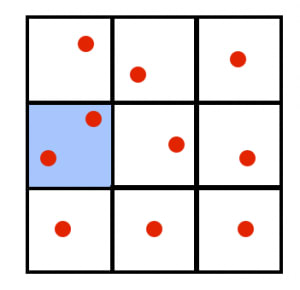
$3\times 3$ の正方形を $1\times 1$ の小正方形 $9$ 個に分割する。鳩ノ巣原理より，$10$ 個の点の中に同じ小正方形に属する $2$ 点が存在する。同じ小正方形に属する $2$ 点の距離は $\sqrt{2}$ 以下なので目標の主張が示された。

直角三角形が存在しないと仮定する。

$E$ を2つに分割したグループ名を $X$，$Y$ と書くことにする。

三辺 $AB,BC,CA$ を $1:2$ に内分する点を $P,Q,R$ とおくと，$AB\perp RP,BC\perp PQ, CA\perp QR$

鳩ノ巣原理により $P,Q,R$ の中で少なくとも2点は同じグループに属する。対称性より，$P,Q$ が $X$ に属するとしても一般性を失わない。

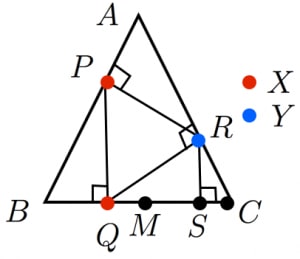
（以下かんたん）

(i)辺 $BC$ 上の $Q$ 以外のある点 $D$ が $X$ に属している場合

三角形 $PQD$ は3点が $X$ に属する直角三角形なので矛盾

(ii)辺 $BC$ 上の $Q$ 以外の全ての点が $Y$ に属している場合

(ii-a) $R$ が $Y$ に属する場合

$R$ から $BC$ に下ろした垂線の足を $S$ とおくと，三角形 $RSC$ は3点が $Y$ に属する直角三角形なので矛盾。

(ii-b) $R$ が $X$ に属する場合

(i)の議論より，$P,Q,R$ 以外全て $Y$ に属す必要がある。このとき $A$ から $BC$ に下ろした垂線の足を $M$ とおくと，三角形 $AMC$ は3点が $Y$ に属する直角三角形なので矛盾。

$23$ 以下の素数は $9$ 個。それぞれの素因数のベキの偶奇でグループわけを行う。つまり，$M$ の要素を $2^9=512$ グループにわける。同じグループのものは掛け合わせると平方数になるので，鳩ノ巣原理から，かけて平方数（$=n_1^2$ ）になるペア $(a_1,b_1)$ が存在する。残り $1983$ 個の数に対しても同様な議論を用いると，かけて平方数（$=n_2^2$ ）になるペア $(a_2,b_2)$ が存在する。

これを（頑張れば730回くらい繰り返せるけど）$513$ 回繰り返してかけて平方数（$=n_i^2$ ）になるペア $(a_i,b_i)$ を $513$ 個作る。

さらに，$n_i$ たちに同様な議論を適用することで $n_in_j$ が平方数（$=n^2$ ）になるようなペアが存在することが分かる。よって，$a_ib_ia_jb_j=n_i^2n_j^2=n^4$ となり目標の主張が示された。

背理法で証明する。各グループに属する個数が $\left\lceil \dfrac{m}{n}\right\rceil-1$ 以下と仮定すると，

個数の合計 $m$ は $n\times\left(\left\lceil \dfrac{m}{n}\right\rceil-1\right)$ 以下である。

つまり，$m\leq n\left(\left\lceil \dfrac{m}{n}\right\rceil-1\right)$

これを変形すると

$\dfrac{m}{n}+1\leq \left\lceil \dfrac{m}{n}\right\rceil$

となるが，これは「$\left\lceil \dfrac{m}{n}\right\rceil$ は$\dfrac{m}{n}$ 以上の最小の整数」に矛盾。