合成積（畳み込み）の意味と応用３つ

合成積（畳み込み）の定義

無限や積分が入っていて一見複雑ですが，畳み込みとは「和が一定となるようなものをかけて足し合わせる」という操作です。

連続版（畳み込み積分）

二つの関数 $f(x)$ と $g(x)$ から以下のような操作をして新しい関数 $h(x)$ を作ります：

$h(x)=\displaystyle\int_{-\infty}^{\infty}f(t)g(x-t)dt$

右辺に $t$ がありますが，積分すると消えるので右辺は $x$ の関数です。

この $h(x)$ を $f(x)$ と $g(x)$ の合成積（畳み込み，畳み込み積分，重畳積分）などと呼びます。合成関数とは全く別の概念です。

$h(x)=f(x)*g(x)$，$h=f*g$ などと書くことが多いです。

離散版（畳み込み和）

数列における畳み込みも同様に定義されます。

$\{ a_n \}$ と $\{ b_n \}$ から以下のような操作をして新しい数列 $\{ c_n \}$ を作ります：

$c_n=\displaystyle\sum_{t=0}^{n}a_tb_{n-t}$

「添字の和が一定となるようなものをかけて足し合わせる」です。

この $\{ c_n \}$ を $\{ a_n \}$ と $\{ b_n \}$ の合成積，畳み込み，畳み込み和などと呼びます。 $c_n=a_n*b_n$，$c=a*b$ などと書くことが多いです。

意味

畳み込みは「和が一定となるようなものをかけて足し合わせる」操作でした。ある点を中心に逆向きにかけて足し合わせたものとも言えます。

このある点を中心に逆向きにかけて足し合わせたものが数学のいろいろな場面で登場するのです。

2次元の畳み込み

多次元の場合も畳み込みを考えることができます。1次元の場合と同じく，畳み込みとはある点を中心に逆向きにかけて足し合わせたものというイメージを持っておくとよいです。図は2次元の場合のイメージです。

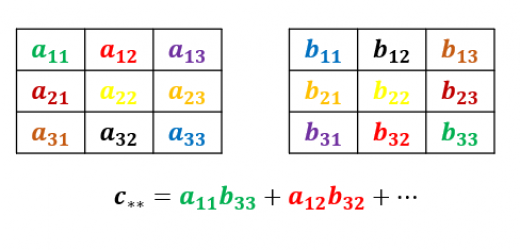
なお，畳み込みニューラルネットワーク(CNN)では2次元の畳み込みを考えます。CNNの畳み込みを考えるときは「逆向き」というイメージよりも「スライドさせながら，対応する要素の積和を計算する」というイメージを持っているとよいです。

応用

合成積（畳み込み）の構造はいろいろなところに出現します。

多項式の積

多項式 $a_nx^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0$ と $b_mx^m+b_{m-1}x^{m-1}+\cdots +b_1x +b_0$ の積の係数は $a$ と $b$ の畳み込みになっています。

これは考えてみれば当たり前ですが，たまに役立ちます。例えば「原始多項式の積が原始多項式であること」の証明の見通しがよくなります。→原始多項式とその積について

確率変数の和の確率

確率変数 $X$ と $Y$ の確率分布が分かっているときに $X+Y$ の確率分布は合成積で与えられます。

• 離散版の場合： $P(X+Y=k)=\displaystyle\sum_{t}P(X=t)P(Y=k-t)$

• 連続版の場合： $X+Y$ の確率密度関数が $X$ の確率密度関数と $Y$ の確率密度関数の合成積になります。確率密度関数の意味と具体例

信号処理

詳細は述べませんが，線形時不変システムという都合のよいシステムならシステムの出力はインパルス応答（あらかじめ求めておける）と入力の合成積で求まるという性質が成立します。

また，合成積はフーリエ変換，ラプラス変換とも相性がよく，信号処理論で重要な役割を果たします。

その他

他にもカタラン数が満たす漸化式やヴァンデルモンドの畳み込みなど，畳み込みっぽい構造はいろいろなところに出現します。 →カタラン数の意味と漸化式 →ヴァンデルモンドの畳み込みの証明

補足

この節は連続版で説明しますが離散版も全く同様です。

• 畳み込みは可換です。つまり，$f*g=g*f$ です。これは畳み込みの意味を考えれば当たり前ですが，以下のように置換積分を用いても簡単に証明できます。

• 畳み込み積分の定義において，積分区間は $-\infty$ から $\infty$ となっていますが，状況によっては和を取る区間を制限する場合もあります。特に信号処理の文脈では周期関数の畳み込みが重要ですが，そのような場合には積分区間を一周期ぶんにとります。

絶対収束する級数における畳み込み和

数列 $a_n$ と $b_n$ の畳み込みを $c_n=\displaystyle\sum_{t=0}^{n}a_tb_{n-t}$ とします。$\displaystyle \sum_{n=0}^{\infty} a_n$，$\displaystyle \sum_{n=0}^{\infty} b_n$ がどちらも絶対収束すれば， $$\sum_{n=0}^{\infty} c_n = \left(\sum_{n=0}^{\infty} a_n\right) \left(\sum_{n=0}^{\infty} b_n\right)$$ となります。

なお，絶対収束については，絶対収束と条件収束の意味と具体例 を参照してください。