カタラン数の意味と漸化式

更新日時 2023/10/23

カタラン数は場合の数の問題で頻繁に登場します！

カタラン数

カタラン数とは， $c_n=\dfrac{{}_{2n}\mathrm{C}_{n}}{n+1}$ で定義される数 $c_n$ のこと。

右辺の ${}_{2n}\mathrm{C}_n$ は二項係数です。 $\dfrac{(2n)!}{n!n!}$ のことです。カタラン数を表す $c$ は小文字，二項係数を表す $\mathrm{C}$ は大文字です。

カタラン数の漸化式・性質

定理1（漸化式）

$c_0=1,\:c_{n+1}=\displaystyle\sum_{i=0}^nc_ic_{n-i}$

証明を2通り紹介します。

母関数を使って漸化式を解く方法。→数列の母関数とその応用例
経路を数える方法。この記事の定理3の証明のあとで紹介します。

定理2

$c_n={}_{2n}\mathrm{C}_n-{}_{2n}\mathrm{C}_{n-1}$

証明

二項係数の定義より，

$\begin{aligned}&{}_{2n}\mathrm{C}_n-{}_{2n}\mathrm{C}_{n-1}\\ &=\dfrac{(2n)!}{n!n!}-\dfrac{(2n)!}{(n-1)!(n+1)!}\\ &=\dfrac{(2n)!}{(n-1)!n!}\left(\dfrac{1}{n}-\dfrac{1}{n+1}\right)\\ &=\dfrac{(2n)!}{n!n!}\times\dfrac{1}{n+1}\\ &=\dfrac{{}_{2n}\mathrm{C}_n}{n+1}\end{aligned}$

最短経路とカタラン数

定理3

$(x,y)$ 座標平面上で $(0,0)$ から $(n,n)$ まで格子点をたどって進む最短経路のうち，常に $x\geqq y$ 部分を通るものの数 $a_n$ はカタラン数と一致する。

証明

場合分けで $a_{n+1}$ を数える。

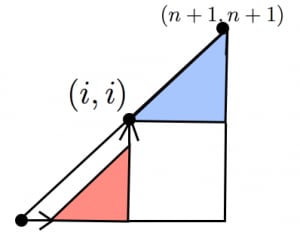
カタラン数と最短経路

左下の点 $(0, 0)$ からスタートして対角線をはじめて $(i, i)$ で踏み， $(n+1, n+1)$ まで到着する場合の数は， $a_{i-1}a_{n+1-i}$ 通り。

これを $i=1$ から $n+1$ まで足し上げるとカタラン数の漸化式と一致する。

では，定理2と定理3を使って定理1（漸化式）を証明します。

定理1の証明

$(0,0)$ から $(n,n)$ までの最短経路の総数は ${}_{2n}\mathrm{C}_n$
そのうち，常に $x\geqq y$ を満たすものが $c_n$ （定理3）

よって，あとは「1回でも $x<y$ を満たす最短経路の数」が ${}_{2n}\mathrm{C}_{n-1}$ であることを示せば良い。これは，以下のように「 $(0,0)$ から $(n-1,n+1)$ への最短経路」と一対一対応が構成できることからわかる：カタラン数の導出 1回でも $x<y$ を満たす $(n,n)$ までの経路に対して「はじめて $y=x+1$ 上を通る点 $A$ 以降を $y=x+1$ に関して折返す」と $(0,0)$ から $(n-1,n+1)$ への最短経路になる。逆に， $(0,0)$ から $(n-1,n+1)$ への最短経路に対して，「はじめて $y=x+1$ 上を通る点 $A$ 以降を $y=x+1$ に関して折返す」と「1回でも $x<y$ を満たす $(n,n)$ への最短経路」になる。

トーナメントとカタラン数

定理4

$n+1$ 人によるトーナメント戦の総数 $a_n$ はカタラン数と一致する（チームは区別せずトーナメントの表だけを考える）。

証明

場合分けで $a_{n+1}$ を数える。

カタラン数とトーナメント

$n+2$ 人でトーナメントをするとき，決勝に左側から上がってくる集団が $i+1$ 人の場合，右側は $n-i+1$ 人。左側のトーナメントのやり方は $a_i$ 通りで，右側は $a_{n-i}$ 通り。これを $i=0$ から $n$ まで足し合わせるとカタラン数の漸化式と一致する。

三角形分割とカタラン数

定理5

へこんでいない $n+2$ 角形に対角線を $n-1$ 本引いて三角形に分割する方法の数 $a_n$ はカタラン数と一致する。

証明

場合分けで $a_{n+1}$ を数える。

カタラン数と三角形分割

$n+3$ 角形の頂点を順番に $A_0, A_1,\cdots, A_{n+2}$ とする。

与えられた三角形分割に対して， $A_{n+1}A_{n+2}A_i$ が分割された三角形の一つであるような $i$ が $0$ から $n$ の間にただひとつ存在する。

それぞれの $i$ について，そのような三角形分割は $a_{i}a_{n-i}$ 通りあり，これを $i=0$ から $n$ まで足し上げると，カタラン数の漸化式と一致する。

カタラン数の意味

カタラン数の意味は，定理1の漸化式
c0=1,cn+1=∑i=0ncicn−ic_0=1, c_{n+1}=\displaystyle\sum_{i=0}^nc_ic_{n-i}c0​=1,cn+1​=i=0∑n​ci​cn−i​
で理解するのが良いです。この漸化式が場合の数の様々な問題で出現します：
最短経路の数（→定理3）
トーナメントの数（→定理4）
三角形分割の数（→定理5）
カタラン数を「特定の場合の数」で理解してしまうと，他の例がわかりにくくなります。例えば「三角形分割の数がカタラン数だ」と覚えてしまうとトーナメントの数とカタラン数の関係が分かりにくくなります。組み合わせによる意味付けはあくまで性質であって，カタラン数とは組み合わせ問題で頻繁に出現する漸化式の解と理解しておくのがよいです。
カタラン数の同様な例としてフィボナッチ数が挙げられます。フィボナッチ数列は「a0=0,a1=1,an=an−1+an−2a_0=0, a_1=1, a_n=a_{n-1}+a_{n-2}a0​=0,a1​=1,an​=an−1​+an−2​
 の解でありいろいろな問題に登場する」と理解しておくとよいです。
→フィボナッチ数列の7つの性質（一般項・黄金比・互いに素）

その他発展的なトピック

母函数

カタラン数の母函数

カタラン数の母函数は $f(x)=\dfrac{1 - \sqrt{1-4x}}{2x}$ である。

つまり $\dfrac{1 - \sqrt{1-4x}}{2x} = \sum_{n=0}^{\infty} \dfrac{{}_{2n} \mathrm{C}_n}{n+1} x^n$ となる。

→ 数列の母関数の意味とその応用例

極限

カタラン数にまつわる極限

$\lim_{n \to \infty} \dfrac{n^{\frac{3}{2}} c_n}{4^n} = \dfrac{1}{\sqrt{\pi}}$

ウォリスの公式 $\prod_{n=1}^{\infty}\dfrac{(2n)^2}{(2n-1)(2n+1)}=\dfrac{\pi}{2}$ を活用します。

証明

$\begin{aligned} \dfrac{1}{4^n} {c_n} &= \dfrac{1}{n+1} \dfrac{(2n)!}{4^n (n!)^2} \\ &= \dfrac{1}{n+1} \dfrac{(2n)!}{((2n)!!)^2}\\ &= \dfrac{1}{n+1} \dfrac{(2n-1)!!}{(2n)!!} \end{aligned}$ と計算される。

二乗したものを考える。

$\begin{aligned} \left( \dfrac{n^{\frac{3}{2}} c_n}{4^n} \right)^2 &= \dfrac{n^3}{(n+1)^2} \left( \dfrac{(2n-1)!!}{(2n)!!} \right)^2\\ &= \dfrac{n^3}{(n+1)^2 (2n+1)} \dfrac{(2n-1)!! (2n+1)!!}{((2n)!!)^2}\\ \end{aligned}$

1項目，2項目の極限を考える。 $\begin{aligned} \lim_{n \to \infty} \dfrac{n^3}{(n+1)^2 (2n+1)} &= \dfrac{1}{2}\\ \lim_{n \to \infty} \dfrac{(2n-1)!! (2n+1)!!}{((2n)!!)^2} &= \dfrac{2}{\pi} \end{aligned}$ （2項目はウォリスの公式による）