数学オリンピックの練習問題(幾何不等式)
1991年国際数学オリンピックスウェーデン大会第一問です。
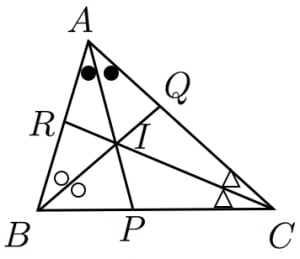
三角形 の内心を , と の交点を , と の交点を , と の交点を とおくとき,
を証明せよ。
幾何不等式について
幾何不等式について
幾何不等式は,図形問題と不等式証明問題を融合したような問題です。数学オリンピックでは幾何不等式は頻出です。幾何不等式にはいくつかの決まった解法パターンがあります。→幾何不等式の解法パターンまとめ
もちろん決まった解法パターンだけで全て解けるわけではありませんが,多くのパターンを知っていると解ける確率が上がります。数学オリンピックでは発想力だけでなく, 多くの問題に通用する解法パターン,テクニックをどれだけ知っているかというのも非常に重要になってきます。
ちなみに,この練習問題の証明では以下のテクニックを使います。
- 三角形の三辺の長さの情報に変換して代数的に証明する
- 不等式が斉次式なら規格化する
- 三辺の長さに関する不等式にはRavi変換
解答はわりと長いですが,やっていることは単純です。数学オリンピックの問題の中では比較的簡単な問題です。
解答(前半)
解答(前半)
まずは,不等式の真ん中の式を三角形の三辺の長さ で表すことが目標になります。角の二等分線と線分比の形から,角の二等分線に関する重要な3つの公式の公式1を使うことが思いつくでしょう。

角の二等分線の公式より,
再び角の二等分線公式より,
よって,
同様にして,
より,以下の不等式を示せばよい。
あとはこの不等式を全力で示すだけです。図形の問題を不等式の問題に変換できました。
解答(右側の不等式)
解答(右側の不等式)
斉次式なので規格化して の場合のみを考えばよいわけです。 で,イカにも相加相乗平均の不等式っぽいです。
のとき を示せばよいが,相加相乗平均の不等式より,
であり,この両辺を三乗すればよい。
解答(左側の不等式)
解答(左側の不等式)
斉次式化はさきほどと同様です。さらに三角形の辺に関する不等式証明の定石であるRavi変換を用います。
のもとで
を示せば良い。ここで, とおくと,三角不等式 などにより, が分かり,示すべき不等式は,
また, より より,
を示せばよいが,この式の右辺を計算すると,
となるので目標の不等式が示された。
なお,示すべき不等式は斉次式なので規格化せずに分母を払ってMuirheadの不等式を用いるという方法も考えられます。しかし,この場合左側の不等式は三角不等式がネックとなってうまくいきません。
斉次式については不等式証明のコツ2:斉次式化も参考にしてみてください。(この問題で使ったテクニック「規格化」は斉次式化の逆の操作になっています。どちらがうまくいくかは問題によります)
小さなテクニックを組み合わせることで大きな問題が解けます。
Tag:幾何不等式の解法パターンまとめ
Tag:国際数学オリンピックの過去問










