正12面体のいろいろな計算（対角線・表面積・体積・内接球・外接球）

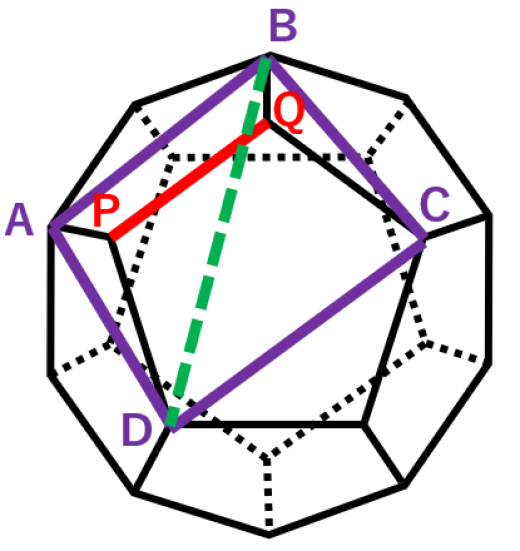
• 1番短いものは辺と一致し，長さ1

• 2番目に短いものは正五角形の対角線の長さなので，$\dfrac{1+\sqrt{5}}{2}$
  （→詳しくは正五角形の対角線の長さと作図方法）

• 3番目に短いものは正方形 $ABCD$ の対角線の長さ。正方形になる理由は，「$AB$ と $CD$ はどちらも $PQ$ と平行なので $A,B,C,D$ は同一平面上にある → さらに4辺の長さが等しいのでひし型 → さらに対称性より $AC=BD$ なので正方形。
  この正方形の1辺の長さは $\dfrac{1+\sqrt{5}}{2}$ だったので，対角線の長さは $\sqrt{2}$ 倍して 長さは $\dfrac{\sqrt{2}+\sqrt{10}}{2}$

4番目に短いものは1辺の長さが $AB$ である正五角形の対角線の長さ。よって長さは $\left(\dfrac{1+\sqrt{5}}{2}\right)^2=\dfrac{3+\sqrt{5}}{2}$

一番長いものは1辺の長さが $AB$ である立方体の対角線の長さになる。（立方体になる理由，つまり各面が正方形になる理由は「3番目に短いもの」の計算で述べた通り。図が見にくいが，正12面体の頂点からうまく8つ選ぶと立方体になる！）

よって長さは $\dfrac{\sqrt{3}+\sqrt{15}}{2}$

正12面体の中心を $O$，正12面体を構成する1つの五角形 $ABCDE$ の重心を $G$ とすると，$OGA$ は直角三角形。

よって，$OG^2+AG^2=AO^2$

ここで，

• $OG$ は内接球の半径 $r$
• $OA$ は外接球の半径 $R$
• $AG=x$ は，頂角が $72^{\circ}$ である二等辺三角形 $OAB$ に余弦定理を使うと，
  $1^2=x^2+x^2-2x^2\cos 72^{\circ}$
  ここで $\cos 72^{\circ}=\dfrac{\sqrt{5}-1}{4}$ より（詳しくは覚えておくと便利な三角比の値），
  $1=x^2\left(2-\dfrac{\sqrt{5}-1}{2}\right)$
  $x^2=\dfrac{2}{5-\sqrt{5}}=\dfrac{5+\sqrt{5}}{10}$

以上から，

$r^2=R^2-x^2\\ =\dfrac{3+15+6\sqrt{5}}{16}-\dfrac{5+\sqrt{5}}{10}\\ =\dfrac{45+15\sqrt{5}-20-4\sqrt{5}}{40}\\ =\dfrac{25+11\sqrt{5}}{40}$

$r=\sqrt{\dfrac{25+11\sqrt{5}}{40}}$

正五角形について，中心と各頂点を結んで合同な三角形5つに分割すると，

$s=5\times\dfrac{1}{2}x^2\sin 72^{\circ}$

である。さきほど計算したように $x^2=\dfrac{5+\sqrt{5}}{10}$ であり，

$\sin 72^{\circ}=\sqrt{1-\cos^2 72^{\circ}}\\ =\sqrt{1-\dfrac{6-2\sqrt{5}}{16}}\\ =\dfrac{\sqrt{10+2\sqrt{5}}}{4}$

なので，

$s=\dfrac{5+\sqrt{5}}{4}\times\dfrac{\sqrt{10+2\sqrt{5}}}{4}$

分子は

$\sqrt{(5+\sqrt{5})^2\times (10+2\sqrt{5})}\\ =\sqrt{5(\sqrt{5}+1)^2\times 2\sqrt{5}(\sqrt{5}+1)}\\ =\sqrt{10\sqrt{5}(\sqrt{5}+1)^3}\\ =\sqrt{10\sqrt{5}(5\sqrt{5}+15+3\sqrt{5}+1)}\\ =\sqrt{10\sqrt{5}\times 8(\sqrt{5}+2)}\\ =\sqrt{16\times 5(5+2\sqrt{5})}\\ =4\sqrt{25+10\sqrt{5}}$

よって，正12面体の表面積は $S=3\sqrt{25+10\sqrt{5}}$

内接球の半径 $r=\sqrt{\dfrac{25+11\sqrt{5}}{40}}$ と表面積 $S=3\sqrt{25+11\sqrt{5}}$ および，$V=\dfrac{1}{3}rS$ より，

$V=\dfrac{1}{3}rS\\ =\dfrac{1}{3}\sqrt{\dfrac{25+11\sqrt{5}}{40}}\times 3\sqrt{25+10\sqrt{5}}\\ =\dfrac{1}{2}\sqrt{\dfrac{(25+11\sqrt{5})(5+2\sqrt{5})}{2}}\\ =\dfrac{1}{2}\sqrt{\dfrac{5(5\sqrt{5}+11)(\sqrt{5}+2)}{2}}\\ =\dfrac{1}{2}\sqrt{\dfrac{5(47+21\sqrt{5})}{2}}\\ =\dfrac{\sqrt{5}}{4}\sqrt{94+2\sqrt{5\times 21^2}}\\ =\dfrac{\sqrt{5}}{4}(\sqrt{49}+\sqrt{45})\\ =\dfrac{15+7\sqrt{5}}{4}$

（最後から2つめの等号で二重根号が外せた！）