正四面体の中心角の2通りの求め方

更新日時 2021/03/07

正四面体 $ABCD$ の中心を $G$ とする。このとき，正四面体の中心角 $\theta=\angle AGB$ は，

$\cos\theta=-\dfrac{1}{3}$ を満たす。

具体的には， $\theta\fallingdotseq 109.5^{\circ}$

正四面体の中心角とは
重心の性質を用いた証明
立方体を用いた証明（きれい！）
マラルディの角度

正四面体の中心角とは正四面体では，
外心（外接球の中心）
内心（内接球の中心）
重心（位置ベクトルの平均）
垂心（頂点から対面に降ろした垂線の交点）
は全て一致します。この点を「中心」と呼ぶことにします。
この記事では，∠AGB\angle AGB∠AGB
 のことを「中心角」と呼びます。
以下では，cos⁡∠AGB=−13\cos\angle AGB=-\dfrac{1}{3}cos∠AGB=−31​
 であることを2通りの方法で証明します。

重心の性質を用いた証明1辺が
111
 の正四面体について考えます。
1辺が
111
 の正三角形の面積が
34\dfrac{\sqrt{3}}{4}43​​
1辺が
111
 の正四面体の体積が
212\dfrac{\sqrt{2}}{12}122​​
であることを使います。→正三角形の面積，正四面体の体積
証明
AAA
 から三角形
BCDBCDBCD
 に下ろした垂線の足を
HHH
 とする。
このとき，
34×AH×13=212\dfrac{\sqrt{3}}{4}\times AH\times \dfrac{1}{3}=\dfrac{\sqrt{2}}{12}43​​×AH×31​=122​​
 より，
AH=23=63AH=\dfrac{\sqrt{2}}{\sqrt{3}}=\dfrac{\sqrt{6}}{3}AH=3​2​​=36​​
また，四面体の重心の性質より，AG:GH=3:1AG:GH=3:1AG:GH=3:1
 であるので，
AG=34AH=64AG=\dfrac{3}{4}AH=\dfrac{\sqrt{6}}{4}AG=43​AH=46​​
対称性より，BG=64BG=\dfrac{\sqrt{6}}{4}BG=46​​
よって，三角形
ABGABGABG
 に余弦定理を使うと，
cos⁡θ=AG2+BG2−AB22AG⋅BG=616+616−12⋅616=−13\cos\theta=\dfrac{AG^2+BG^2-AB^2}{2AG\cdot BG}\\
=\dfrac{\frac{6}{16}+\frac{6}{16}-1}{2\cdot\frac{6}{16}}\\
=-\dfrac{1}{3}cosθ=2AG⋅BGAG2+BG2−AB2​=2⋅166​166​+166​−1​=−31​
※ 余弦定理を使わないもう少し楽な方法もあります。重心の性質から cos⁡∠HGB=13\cos\angle HGB=\dfrac{1}{3}cos∠HGB=31​ がわかり，これと θ+∠HGB=180∘\theta+\angle HGB=180^{\circ}θ+∠HGB=180∘ から cos⁡θ=−13\cos\theta=-\dfrac{1}{3}cosθ=−31​ がわかります。

立方体を用いた証明（きれい！）

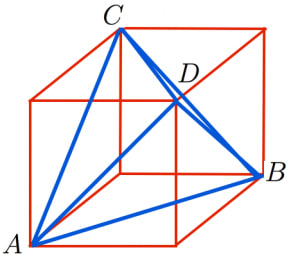
正四面体in立方体

立方体の4つの頂点をうまく選ぶことで，正四面体を構成できます。→正四面体の体積を計算する

これを利用すれば $\cos\theta=-\dfrac{1}{3}$ を非常に簡単な計算で示せます。

証明

座標空間上に正四面体 $ABCD$ を以下のように構成する:

$A(0,0,0)$ ， $B(2,2,0)$ ， $C(2,0,2)$ ， $D(0,2,2)$

このとき，正四面体の中心 $G$ の座標は $(1,1,1)$ となる。

$\overrightarrow{GA}=(-1,-1,-1)$

$\overrightarrow{GB}=(1,1,-1)$

より，

$\cos\theta=\dfrac{\overrightarrow{GA}\cdot\overrightarrow{GB}}{|\overrightarrow{GA}||\overrightarrow{GB}|}\\ =\dfrac{-1-1+1}{\sqrt{3}\cdot\sqrt{3}}\\ =-\dfrac{1}{3}$

マラルディの角度

今回求めた $109.5^{\circ}$ に近い角度をマラルディの角度と言います。マラルディの角度は正四面体の中心角だけでなく，他のいろいろなところにも登場します。

例えば，A4用紙の対角線のなす角（のうち鈍角の方） $\theta$ は，マラルディの角度と一致します。実際，A4用紙の縦横比が $\sqrt{2}:1$ であることから $\cos\theta=-\dfrac{1}{3}$ がわかります。

正四面体の「中心角」という言葉の使い方は一般的では無い気がします。

この記事の編集者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！