錐体の体積に1/3がつくことの2通りの説明
更新
三角錐,四角錐,円錐などの錐体の体積は
底面積が ,高さが である錐体の体積 を求める公式: の導出を紹介します。
特殊な四角錐の場合
特殊な四角錐の場合
底面が一辺 の正方形であるような特殊な正四角錐の場合は,立方体を六個に切ることで簡単に が証明できます。
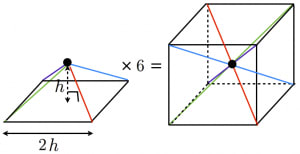
底面積は
高さは
また,一辺 の立方体から同じ形の立体が六個取り出せるので,体積は
以上より, が分かる。
一般の錐体の場合
一般の錐体の場合
次に,底面積が ,高さが の一般の錐体 の体積 について考えます。
底面が一辺 の正方形であるような特殊な四角錐 の体積は でした( は の底面積)。
この二つの立体を底面からの距離が の平面で切ると,その断面積の比は常に です。 よって,体積の比も になります。
つまり,求めたい の体積は となります。
積分を用いた証明
積分を用いた証明
二つ目の説明です。数学2の知識が必要になります。積分を使って を証明します。底面積の形によらない(円錐でも三角錐でも四角錐でも適用可能)証明方法です。
底面からの距離が であるような平面で錐体を切ったときの断面積を とする。
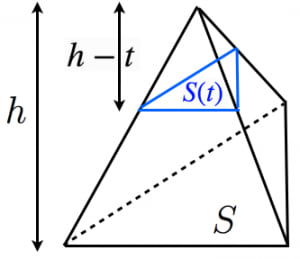
が十分小さいとき,底面からの距離が から の間にある部分の体積は とみなせるので,
また,相似な図形の面積比は相似比の二乗に比例するので,
よって,
以上より,
最後の証明,底面からの距離でなく頂点からの距離を にすればよかったと後悔しています。











