円の接線の方程式を求める公式の3通りの証明
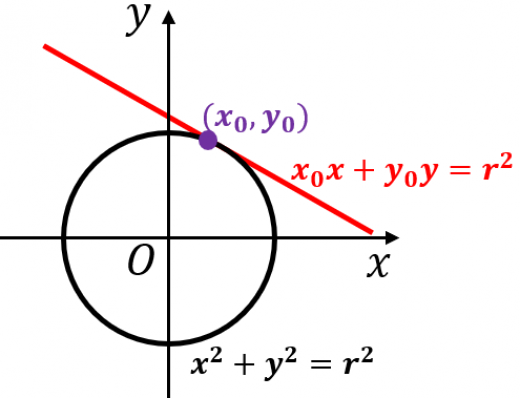
座標平面において,円: 上の点 における接線の方程式は,
円の接線の方程式を求める公式について,例題と3通りの証明を整理しました。
例題
例題
まずは,具体例で円の接線の方程式を求めてみましょう。
円 上の点 における接線の方程式を求めよ。
公式 に対して とすればよいので,
が答え。
円の中心が原点でない場合
円の中心が原点でない場合
座標平面において,円: 上の点 における接線の方程式は,
これは原点を中心とするバージョンを「平行移動」するだけで簡単に導出できます。極線の方程式でやっていることと全く同じなので平行移動バージョンの証明は省略します。
以下では,原点中心の場合の公式 を3通りの方法で証明します。
1.傾きと通る点から求める方法
1.傾きと通る点から求める方法
まずは素直な証明方法です。
・ のとき
における接線は,直線 と直交するので,その傾きは である。
よって,通る一点と傾きが分かったので求める方程式は,
と分かる。
これを整理すると,
また, は円上の点であることから
以上より求める方程式は
・ のいずれかが であるときも簡単に確認できる。
2.法線ベクトルを用いる方法
2.法線ベクトルを用いる方法
法線ベクトルについて知っていれば簡単に証明できます。この方法はややレベルが高いですが,楕円などにも応用できる素晴らしい方法です。
ベクトル は,点 における円の法線ベクトルである(図形的に分かるし,偏微分からも分かる)。
よって(定数 を用いて)接線の方程式は と書ける。
これが, を通るので,
以上より求める接線の方程式は
3.距離公式を用いる方法
3.距離公式を用いる方法
点と直線の距離公式を使って証明することもできます。
この状況ではあまりスマートではない(証明1の下位互換な気もする)方法ですが,円の接線は距離公式から求まるという考え方は大事です。
の場合のみ証明する。
を通る方程式は,
つまり, (*)と書ける。
この直線と原点の距離が になるとき,接線の方程式となるので,点と直線の距離公式より,
に注意して上式を変形していく:
よって,
求める方程式は,(*)に代入して整理すると となる。
ちなみに,楕円の場合(この公式の一般化)については楕円の接線を求める公式とその証明をどうぞ。
「円の接線の方程式の公式の3通りの証明」というタイトルにしようと思ったのですが「の」ばっかりだったので少し変えました。











