極線の方程式の証明と応用
円 に対して,外側の点 から引いた2本の接線の接点を とおく。
- 直線 を(極 に対する)極線と呼ぶ。
- 極線の方程式は
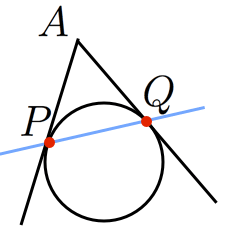
極と極線について整理しました。
極線の方程式の計算例
極線の方程式の計算例
極線の方程式を求める問題は大学入試で頻出です。
円 に対して から引いた2本の接線の接点を とおく。直線 の方程式を求めよ。
極線の方程式の公式 を使うと,求める方程式は となる。
このように,極線の方程式を一発で求めることができます(公式を使わずに接点 の座標を計算で求めようとすると大変)。
公式の証明
公式の証明
極線の方程式が になることを証明します。
独特な証明方法ですが重要なので,理解するまでじっくり考えてみてください。
接点の座標をそれぞれ , とおき,, が 上にあることを言えばよいです。

という式は
- 左辺が の一次式であり直線を表す。
- 後ほど証明(※)するように, を通る。同様に も通る。
を通る直線は一本しかないので こそが求める極線である。
※ を通ることの証明
上の点
における接線の方程式は,
これが点
を通るとき,
を満たす。つまり,
上に点
がある。
二次曲線の極線
二次曲線の極線
楕円・双曲線・放物線でも同様に極線を考えることができます。
二次曲線に対して, から引いた2本の接線を引けるとし,その接点を とおく。直線 を(極 に対する)極線と呼ぶ。
- 楕円 の極線の方程式は
- 双曲線 の極線の方程式は
- 放物線 の極線の方程式は
極線の方程式の導出は,円の場合と同じ考え方でできます。
について から放物線 に2本の接線を引き,接点を とする。直線 の方程式が であることを示せ。
放物線 と極 に対して極線の方程式の公式を使うと,
また,放物線の極線については,以下のおもしろい定理が成立します。
放物線外の点 と, から放物線に引いた2本の接線の接点 について,以下は同値。
- と は垂直
- は放物線の準線上にある
- 極線 上に焦点 がある
- と は垂直
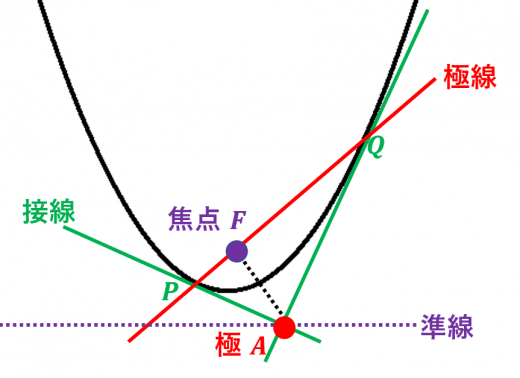
ぜひ証明してみてください。放物線の焦点と準線については放物線の準線・焦点と一般化をどうぞ。
円の中心が一般の場合の極線の方程式
円の中心が一般の場合の極線の方程式
円の中心が原点でない場合も含めて,以下が成立します。
円 とその外側の点 に関する極線の方程式は, である。
原点中心の場合の結果とグラフの平行移動を用いて証明できます。
図形全体を 軸方向に , 軸方向に 平行移動して円の中心を原点にずらす:
円:
外側の点:
よってさきほどの結果より,これらに対する極線の方程式は
これを元に戻す( 軸方向に , 軸方向に 平行移動)
すると求める極線の方程式が得られる!
極線の方程式の応用
極線の方程式の応用
極線にまつわる重要な性質を紹介します。
点 ,円 ,極線を とする。円 と2点 で交わり極線と で交わるような を通る直線を考える。
すると, ( は調和点列である)
- この性質を証明せよと入試で出題されたことがあります!
- 数学オリンピックの問題でたまに使える性質です!
ここでは極線の方程式を使って機械的な座標計算で証明します(解と係数の関係を用いることで計算量を減らすことができます)。

と座標を設定する。
目標は だが,長さを計算するのは面倒なので全て 座標の比率で考える(注1)
- 極線の方程式は より の 座標は
- 直線と円の方程式を連立させて を消去すると,
なので の 座標を として
解と係数の関係より
ここで,目標は,
なので上記の結果を代入して左辺を計算すると確かに成立していることが分かる。
注1:長さの比は 方向の距離の比と等しいです。
注2:細かい計算は省略したのでぜひとも一度手を動かして確認してみてください。
追記
「極線と調和点列」の美しい証明を読者の方に教えてもらいました。

接弦定理より,
( とおく)
( とおく)
とおく
とおく
すると(頂点 を含む)三角形の面積比に注目することで
( であることを用いた)
同様に(頂点 を含む)三角形の面積比に注目することで
以上2つの式より( かつ なら なので) である。
放物線の極線については,阪大の問題含めて高校時代の恩師のy先生に教えていただきました。また,最後の美しい証明は読者の方に教えていただきました。ありがとうございます!











