平面,空間上の2点間の距離について

2点間の距離(平面あるいは空間内にある2点を結ぶ線分の長さ)を,点の座標で表す公式を紹介します。
2点間の距離の公式
2点間の距離の公式
平面・空間内の2点間の距離を求める公式です。入試問題などでも頻繁に使う公式ですので,暗記しましょう。
平面内の2点 の間の距離 は で与えられる。
また,空間内の2点 の間の距離 は で与えられる。
考えている座標の 座標, 座標,( 座標) ごとに引き算をする点に注意してください。
原点との距離の求め方
特に,原点との距離は公式として覚えておくと便利です。上式から導出できます。
- 2次元の場合
- 3次元の場合
となります。
具体例
具体例
いくつかの具体例で,公式の使用例を確認してみましょう。

平面内の2点 の間の距離 は
です。
空間内の2点 の間の距離 は
です。
2点間の距離の公式の証明
2点間の距離の公式の証明
三平方の定理をうまい三角形に使うことで線分の長さを計算します。→三平方の定理
- 平面の場合
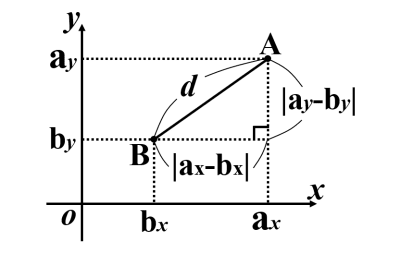
図のように,線分 を斜辺とする直角三角形に対して三平方の定理を使うと,
となるので,この式の平方根をとればよい。
- 空間の場合

点 から,「点 を通り 平面に平行な平面 」 へ下ろした垂線の足を とおくと, である。このとき平面の場合の式より,線分 の長さは
で与えられる。また線分 の長さは である。よって三角形 に三平方の定理を使うと
となるので,この式の平方根をとればよい。
証明からわかるように,平面の場合は実質的に三平方の定理そのものです。
公式とみるか,定義とみるか?
公式とみるか,定義とみるか?
ここから発展的な話題です。
我々が普段考える「距離」の概念からすると,
2点 の間の距離 は式 で表される
という主張は,まず「距離」というものの定義があって,それに基づいて証明されるべき公式(定理)です。実際にこの記事では三平方の定理を使った証明を紹介しました。現実世界で計算する分にはこれでほとんど問題ありません。
しかし数学的に厳密な「距離」や「線分の長さ」の定義とはなんでしょうか?よく考えてみるとなかなか難しい問題です(「極限」を考えるときにも似たような問題が現れていました。→はさみうちの原理の証明,イプシロンデルタ論法とイプシロンエヌ論法)
この問題は,発想を逆転させてこの式そのものを距離の定義として採用することによって解決します。つまり,2点 の間の距離とは, のことであるとしてしまうのです。この立場からみると,2点間の距離の公式はもはや定理ではなく距離の定義そのものになります。→ルール(定義)と事実(定理)を区別する
いろいろな距離
いろいろな距離
と の間の距離とは のことである,という立場に立つと「他の形の式を距離の定義とすることはできるのか?」という自然な疑問が湧いてきます。実は他にもいろいろな距離の定め方があります。
-
距離は, と の間の距離を で測るような距離です。
-
距離は, と の間の距離を で測るような距離です。
詳しくは→L1距離(マンハッタン距離)の意味と性質,ノルムの意味とL1,L2,L∞ノルムを参照してください。
平面や空間の点に限らないものとしては,例えば
- 関数や数列の間の距離を測る 距離
- 文字列の間の距離を測るハミング距離,レーベンシュタイン距離
などがあります。
さらに詳しく知りたい方は,距離空間というキーワードで調べてみてください。
まさに発想のコペルニクス的転回です。









