回転放物面の方程式と東大の問題
放物線をその軸に関して回転させたときにできる図形を回転放物面と言う。
座標空間において,放物線 を 軸のまわりに回転させたときにできる図形の方程式は である。
回転放物面に関する基本的な知識および関連する東大の入試問題を解説します。
回転放物面について
回転放物面について

- まずは放物線を回転させた図形「回転放物面」なるものをイメージしてみてください。おわんのような形をしています。
- 「回転放物面の対称軸に対して平行に入射した光は全て焦点に集まる」というよい性質があるのでパラボラアンテナに使われています。
- というタイプの式は, のとき楕円放物面 のとき双曲放物面 と呼ばれる図形を表します。回転放物面は楕円放物面の特殊な場合( の場合)です。
回転放物面の方程式
回転放物面の方程式
冒頭の主張をより一般化した形で説明します:
偶関数 を 軸のまわりに回転させたときにできる図形の方程式は, である。
この補題に を適用すれば冒頭の主張が得られます。
と は回転軸からの距離が等しい。
よって, における の値は における の値と等しく,その値は である。
よって,求める方程式は
である。
注1: が偶関数でないと,回転させたときに対応する が二つでて来てしまったりしてめんどう&考える意味がなさそうなので,偶関数という条件をつけました。
注2:この補題は当たり前に見える人もいると思いますが,記述式の試験で使うときは簡単に説明を添えた方がよいでしょう。
1983年東大理系第6問
1983年東大理系第6問
回転放物面の式を知っているとやや有利(知らない場合は上記の考え方で導けばよいだけですが)になる東大の問題です。
東大入試の中でも難し目の問題です。
放物線 を 軸の回りに回転させて得られる曲面 を原点を通り回転軸と の角をなす平面 で切る。曲面 と平面 で囲まれた部分の体積を求めよ。
おわんにみそ汁を入れて 傾けると体積を求めるべき図形の形がなんとなく分かります。
この記事では 軸を回転軸としてきましたが,東大の問題では 軸を回転軸としているので,補題においても と の役割が入れ替わります。
は一意には定まりませんが,どの方向から切っても同じなので, 軸と平行なものを取ってくれば計算が楽です。
回転放物面 の方程式は,
平面 の方程式は,法線ベクトルが なので, →平面の方程式とその3通りの求め方
よって, 軸に垂直な平面 で切った切り口(注1)は
で表される領域。(以下は回転放物面の知識は関係ありません)
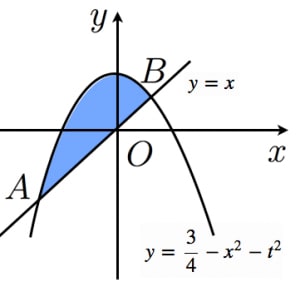
また,図の の 座標は を解いて,
よって,青い図形が存在するような の範囲は であり,そのときの青い図形の面積は 公式(注2)より
よって,求める体積は
と置換するなりして計算すると となる。
注1: で切ってもできます。 で切ると多分できません。
これからはパラボラアンテナを見つけたら「お,回転放物面だ!」と思えますね。










