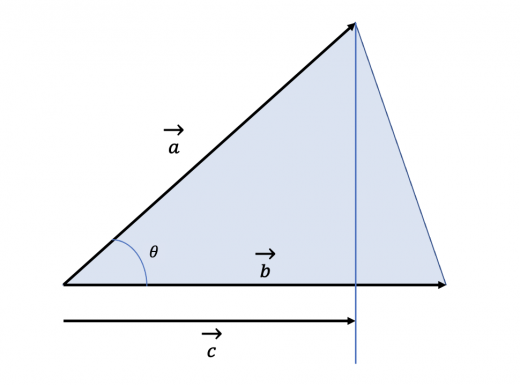
内積の成分表示
ベクトルの内積は「長さとなす角による定義」から計算できますが,ベクトルの成分がわかっていればそこから計算することもできます。
内積の成分表示(2次元)
a の成分を (a1,a2),b の成分を (b1,b2) とする。このとき,二つのベクトル a,b の内積は以下のようになる。
a⋅b=a1b1+a2b2
ここでは2次元のベクトルの内積を扱ったので成分は2つでしたが,3次元のベクトルの内積についても,対応する成分の積の和 a1b1+a2b2+a3b3 で求めることができます。
2つのベクトルのなす角の求め方
内積は,a⋅b=∣a∣∣b∣cosθ で定義されました。これを cosθ について解くと,以下のようになります。
なす角の求め方
cosθ=∣a∣∣b∣a⋅b
つまり,内積 a⋅b とそれぞれの長さからなす角を計算できます。
ベクトルの平行条件
以下,2つの 0 でないベクトル a=(a1,a2),b=(b1,b2) について考えます。
ベクトルの平行条件
以下は同値。
- 2つのベクトル a,b が平行
- ∣a⋅b∣=∣a∣∣b∣
- a1b2−a2b1=0
ベクトルの平行条件の証明
1つめの証明
2つのベクトル a と b が平行
⟺ 2つのベクトルのなす角 θ は 0° または 180°
⟺ cosθ=±1
⟺ ∣∣a∣∣b∣cosθ∣=∣a∣∣b∣
⟺ ∣a⋅b∣=∣a∣∣b∣
2つめの証明
∣a⋅b∣=∣a∣∣b∣
⟺ (a⋅b)2=∣a∣2∣b∣2
⟺(a1b1+a2b2)2=(a12+a22)(b12+b22)
⟺(a1b2−a2b1)2=0
⟺a1b2−a2b1=0
ベクトルの垂直条件
ベクトルの垂直条件
以下は同値。
- 2つのベクトル a,b が垂直
- a⋅b=0
- a1b1+a2b2=0
ベクトルの垂直条件の証明
1つめの証明
内積の定義より,
a⋅b=∣a∣∣b∣cosθ
二つのベクトルが垂直である時,なす角は 90° であるので cosθ=0 よって
a⋅b=0
2つめの証明
1つめと内積の成分表示:a⋅b=a1b1+a2b2 からわかる。
内積を用いた三角形の面積の求め方
△OAB の面積 S は,二つのベクトル OA=(a1,a2),OB=(b1,b2) を用いて以下のように表せます。
三角形の面積の求め方
S=21∣OA∣2∣OB∣2−(OA⋅OB)2
2.
S=21∣a1b2−a2b1∣
1の証明
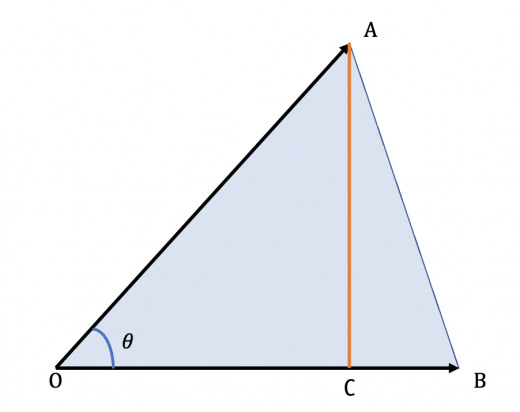
図のように C を定めると,この三角形の面積は S=21×∣OB∣×∣AC∣
となる。また,∣AC∣=∣OA∣sinθ であるので,
S=21×∣OB∣×∣OA∣×sinθ
と変形できる。この式を変形すると,
S==21×∣OB∣×∣OA∣×1−cosθ221∣OA∣2∣OB∣2−(OA⋅OB)2
と公式を得る。
2の証明
1の結果と内積の成分表示を用いる。
∣OA∣=(a1,a2),∣OB∣=(b1,b2) とすると,1の式は以下のように変形できる:
S=(a12+a22)(b12+b22)−(a1b1+a2b2)2=a12b22+a22b12−2a1b1a2b2=21∣a1b2−a2b1∣
ここでは内積を用いた三角形の面積について簡単に紹介しました。
内積を使えると数学が楽しくなるので,内積と仲良くなれるようにがんばりましょう。