内分点,外分点の公式と証明
高校数学の教科書のいろいろな分野で登場する内分点,外分点の公式についてわかりやすく説明します。
内分点,外分点の意味
内分点,外分点の意味
内分点と外分点はセットで覚えるとよいです。
内分点とは

線分 を に内分する点 とは,
を満たす点で線分 の内側にあるもの
のことです。
とする。 を に内分する点 に対して の長さは で の長さは である。
特に, のとき,つまり に内分する点は中点です。
外分点とは
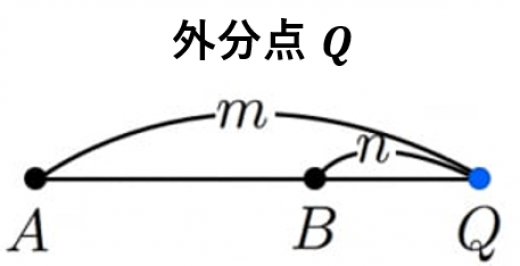
線分 を に外分する点 とは,
を満たす点で線分 の外側にあるもの
のことです。
とする。 を に外分する点 に対して の長さは で の長さは である。
内分点,外分点の公式(座標)
内分点,外分点の公式(座標)
, のとき
-
線分 を に内分する点 の座標は
-
線分 を に外分する点 の座標は
のとき, を に内分する点 の座標と に外分する点 の座標を求めよ。
内分点の公式で として,内分点の座標は
これを計算すると,
同様に,外分点の座標は
これを計算すると,
なお,空間座標の場合は 座標が同じように加わるだけです。
内分点,外分点の公式(ベクトル)
内分点,外分点の公式(ベクトル)
の位置ベクトルを , の位置ベクトルを とするとき,
-
線分 を に内分する点 の位置ベクトルは
-
線分 を に外分する点 の位置ベクトルは
内分点,外分点の公式(複素数平面)
内分点,外分点の公式(複素数平面)
複素数平面において,, とするとき,
線分 を に内分する点 を表す複素数は
線分 を に外分する点 を表す複素数は
証明
証明
座標版,ベクトル版,複素数平面版,それぞれ表現方法は異なりますが全て同じ公式です。証明も同じようにできます。ここではベクトルの言葉で書きます。

内分点
より
であり,右辺を変形すると
となる。
外分点
のときを証明する( のときも同様にできる)。
より
であり,右辺を変形すると となる。
内分点,外分点の公式はよく使うので丸暗記をオススメしますが,このように一瞬で導出できるので忘れても問題ありません。
同じ公式が四回も(座標,平面ベクトル,空間ベクトル,複素数平面)登場することで教科書の紙面を圧迫しています。











