たすきがけによる因数分解のやり方・例題・他の方法
たすきがけとは, のような二次式を因数分解するための方法です。
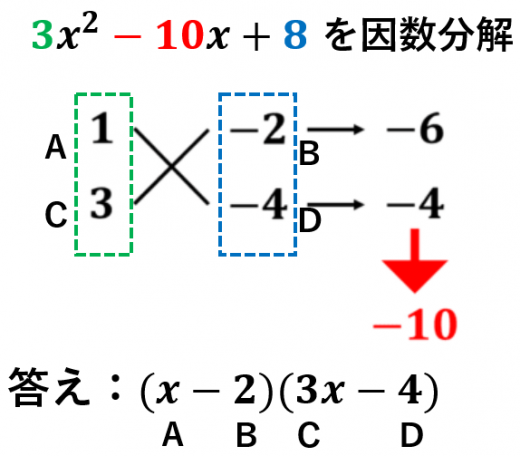
たすきがけによる因数分解のやり方と例題をわかりやすく説明します。
たすきがけによる因数分解
たすきがけによる因数分解
以下の例題を使って,たすきがけのやり方を説明します。
を因数分解せよ。
手順1. かけて (二次の係数)になる2つの整数を適当に決めて左に縦に並べる。例えば, と はかけて になる。

手順2. かけて (定数項)になる2つの整数を適当に決めて右に縦に並べる。例えば と はかけて になる。

手順3. 「たすきがけ(斜めにそれぞれ掛け算)」する。今回の例だと, と のように計算できる。

手順4. 足し算して (一次の係数)になればOK
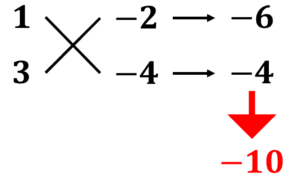
OKの場合,手順1と2で選んだ4つの数を使って因数分解できます:
※手順4でうまくいかない場合(足し算して にならない場合),手順1に戻って別の候補を探します。
最短で得点力を上げる!高校数学の問題集〈典型250問〉の問題7では,たすきがけの問題で計算ミスをしないためのポイントも解説しています。
たすきがけを用いない方法
たすきがけを用いない方法
二次式の因数分解は,たすきがけを用いなくても,二次方程式の解の公式を使って機械的に計算できます。
を因数分解せよ。
という二次方程式の解を,解の公式を使って計算すると
となる。よって, の解が であるとき, と因数分解できる
という性質(※)を使うと,
と因数分解できる。
※上記の性質は,因数定理を使っても証明できますし,直接
を展開して になることを確認することもできます。
たすきがけを用いない方法のメリット
たすきがけを用いない方法のメリット
- たすきがけは直感で「当たり」を見つける必要がありますが,解の公式による方法は機械的に計算できます。そのため, のように数字が大きい場合も,そこまで時間をかけずに確実に因数分解できます。
- 「因数分解せよ」という問題ではきれいに因数分解できるので)解の公式を使っている途中で,ルートの中身が平方数になることを確認できて,自分の計算に自信が持てます。
2変数の例題
2変数の例題
を因数分解せよ。
たすきがけによる解答
まず, の部分をたすきがけで因数分解すると,上式は

となる。さらに,上式でもう一回たすきがけを頑張ると,

となる。
解の公式を使う解答
を解く。まず,解の公式におけるルートの中身は
となり完全平方式になる。
よって,解の公式より
よって,因数分解した結果は
となる。
「たすきがけは不要」とまでは言いませんが,たすきがけを忘れてもなんとかやっていける!











