2平面のなす角の定義と求め方
2つの平面 , のなす角を とすると,
前提知識
前提知識
-
平面の方程式は という1次式で表現できる。
-
というベクトルは,平面 の法線ベクトル(平面と垂直なベクトル)。
これらの知識については平面の方程式とその3通りの求め方を参照して下さい。
以下の議論は2直線のなす角を求める2通りの方法と比較のコサインによる方法を3次元に拡張したものです。
2平面のなす角とは
2平面のなす角とは
まずは2平面のなす角をきちんと定義します。教科書(東京書籍)による定義です。
2平面の交線 上の点 を通り,平面 上にそれぞれ と垂直な直線 を引く。 と のなす角をもとの2平面のなす角とする。
確かに「2平面のなす角」という感じがします。
注:当然ですが,2平面のなす角は の取り方によりません。
冒頭の公式の証明
冒頭の公式の証明
という記号はさきほどの定義内と同じ意味で使います。2平面のなす角はそれぞれの法線方向がなす角と等しいというのがポイントです。
平面 の方程式を , の方程式を とする。
の法線ベクトルは
の法線ベクトルは
ここで,法線ベクトルの定義より,
- は直線 と交線 の両方に垂直
- は直線 と交線 の両方に垂直
よって,
と
のなす角は
方向の直線と
方向の直線のなす角と等しい。
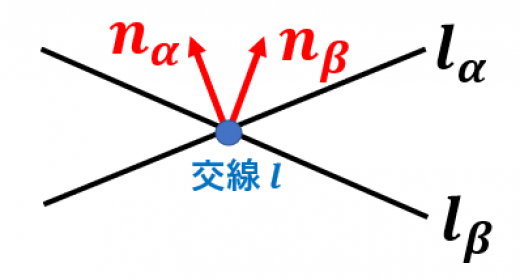 (交線 に垂直な平面を図示した)
(交線 に垂直な平面を図示した)
よって求める角度を とすると,
より,
となり冒頭の公式を得る。
注:ベクトルのなす角は 以上 以下ですが,2平面のなす角は 以上 以下です。(冒頭の公式において)分子には絶対値が必要です。
平面のなす角の意味は直感的には難しくありませんが,きちんと定義を言える人は少ない気がします。











