ロドリゲスの回転公式(行列)
三次元空間における回転行列は,
Rθ=(1−cosθ)⎝⎛nx2nxnynxnznxnyny2nynznxnznynznz2⎠⎞+⎝⎛cosθnzsinθ−nysinθ−nzsinθcosθnxsinθnysinθ−nxsinθcosθ⎠⎞
つまり,三次元空間において,n=(nx,ny,nz) を軸として,r=(x,y,z) を θ 回転させた点の座標は Rθr⊤
例題1(再掲)
点 r=(2,1,0) を軸 n=(1,0,0) のまわりに θ=180∘ 回転させた点の座標を計算せよ。
解答
今度は回転行列を使って計算してみる。cos180∘=−1,sin180∘=0,ny=nz=0 より
Rθ=2⎝⎛100000000⎠⎞+⎝⎛−1000−1000−1⎠⎞=⎝⎛1000−1000−1⎠⎞
よって,回転後の座標は Rθ⎝⎛210⎠⎞=⎝⎛2−10⎠⎞
二次元の回転行列との関係
-
二次元の回転行列 (cosθsinθ−sinθcosθ) はよく使いますね。→一次変換の意味と重要な5つの例(折り返し・回転・対称移動)
-
ロドリゲスの回転公式において,n の向きがいずれかの座標軸の向きと一致する場合,二次元の回転行列が出てきます。例えば n=(0,0,1) とすると,Rθ=⎝⎛cosθsinθ0−sinθcosθ0001⎠⎞ となります。
行列版の導出
ロドリゲスの回転公式(行列)は,ベクトル版から簡単に導出できます。
証明
ベクトル版の公式:
(cosθ)r+(1−cosθ)(r⋅n)n+(sinθ)(n×r)
に各成分を代入すると,
-
第一項は ⎝⎛cosθ000cosθ000cosθ⎠⎞⎝⎛xyz⎠⎞
-
第二項は (1−cosθ)⎝⎛nx2nxnynxnznxnyny2nynznxnznynznz2⎠⎞⎝⎛xyz⎠⎞
-
第三項は ⎝⎛0nzsinθ−nysinθ−nzsinθ0nxsinθnysinθ−nxsinθ0⎠⎞⎝⎛xyz⎠⎞
となり,足し合わせると Rθ⎝⎛xyz⎠⎞
となる。
ロドリゲスの回転公式を最初見たときは「なんかごちゃごちゃしているなあ」と感じましたが,何度も眺めていると「けっこうきれいだなあ」という気持ちになりました。
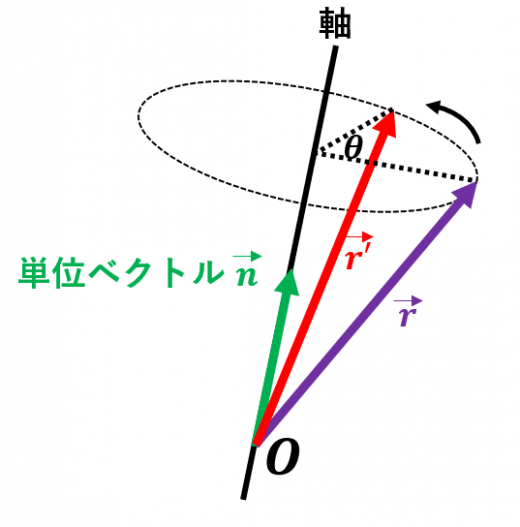 三次元空間において, を軸として, を 回転させた点 は,
三次元空間において, を軸として, を 回転させた点 は,
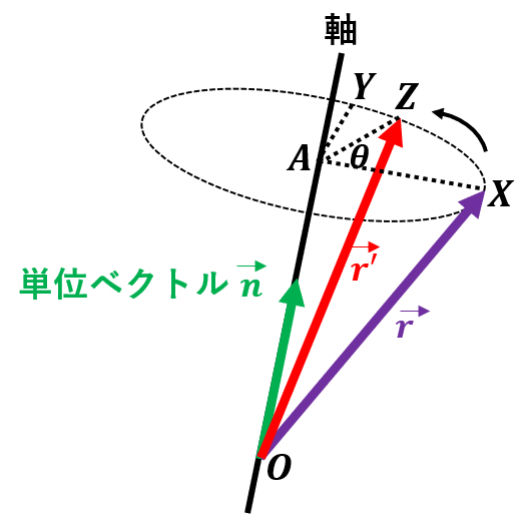 図のように を定める。( は を 回転させた点。 軸が で 軸が である 座標平面をイメージするとよい)
図のように を定める。( は を 回転させた点。 軸が で 軸が である 座標平面をイメージするとよい)










