線分の長さの求め方(2点間・放物線・二等辺三角形・弦)
この記事では座標平面上で線分の長さを求める問題の解き方を解説します。
簡単なパターンからはじめて,放物線や円に切り取られた線分の長さの計算もします。
直線・半直線・線分
直線・半直線・線分
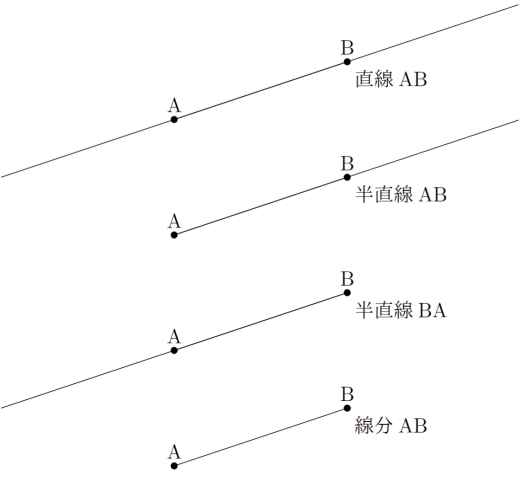
点 と点 を考えます。この2点を通るまっすぐな線の中で,
- どちらの方向にも無限に伸びているものを直線といいます。
- 片方が端になっておりもう片方が無限に伸びているものを半直線といいます。半直線 は が端です。
- 両端で止まっているものを線分といいます。
線分の長さの求め方
線分の長さの求め方
線分の長さは,その2点間の距離です。
平面,空間上の2点間の距離について にあるように,点 と点 に対して,線分 の長さは となります。
実際に例題を解いてみましょう。
座標平面上に2点 , がある。
線分 の長さを求めよ。
2点間の距離の公式を用いる。
つまり長さは
放物線が切り取る線分の長さ
放物線が切り取る線分の長さ
放物線が切り取る線分の長さも計算してみましょう。
座標平面上に二次関数 がある。
- が 軸から切り取る線分の長さを求めよ。
- が直線 から切り取る線分の長さを求めよ。
まずは,方程式を解いて交点を調べてから「2点間の距離公式」を当てはめる方法です。
-
と の交点を求める。二次方程式 の解は である。よって交点は となる。こうして切り取られる線分の長さは となる。
-
と の交点を求める。 の解は である。それぞれの 座標は である。よって線分の長さは となる。
1番はまだしも,2番は計算が複雑でしたね。計算ミスをしそうです。実は計算を簡単にするテクニックがあります。次の別解を見てください。
と の交点の 座標は である。
直線 の傾きが であることから,2交点の線分の長さは 座標の差の 倍になる。
よって線分の長さは である。

このように座標平面上で線分の長さを計算するときは,「うまい方法」で計算量を減らせる場合があります。
最短で得点力を上げる!高校数学の問題集〈典型250問〉 の問題59では,この問題の類題と計算ミスを減らすコツを紹介しています。
二等辺三角形と線分の長さ
二等辺三角形と線分の長さ
先ほどのケースのような「うまい方法」の1つに二等辺三角形の性質を用いるものがあります。
早速例題を見てみましょう。
座標平面上に2点 , がある。
2点 , と等距離にある 軸上の点 の座標を求めよ。
まずは素直に計算してみましょう。
とおく。2点間の距離の公式により である。 より である。両辺を2乗して が得られる。これを解くと ,すなわち が得られる。
タイトル通り,二等辺三角形を活用してみましょう。
条件から でした。これは三角形 が二等辺三角形であることを意味します。
ここで から辺 に垂線をおろすとその足はどのような点になるでしょうか?
から辺 に垂線をおろした足を とおく。
条件から であるため,三角形 は二等辺三角形である。よって は辺 の中点になる。
よって, となる。
直線 の傾きは である。直線 と直線 は直交するため,直線 の傾きは である。
よって直線 は, を通り傾き の直線であるから,その式は である。 は 軸上の点であるため,上の直線の式に を代入すると が得られる。こうして である。
このように二等辺三角形の構図を利用することも多いです。覚えておきましょう。
弦の長さ(円が切り取る線分の長さ)
弦の長さ(円が切り取る線分の長さ)
線分の長さの派生として,弦の長さの求め方を考えていきます。
弦とは円周上に両端点を持つ線分です。
実は弦の長さの計算では,先ほど紹介した二等辺三角形の活用がダイレクトに効いてきます。
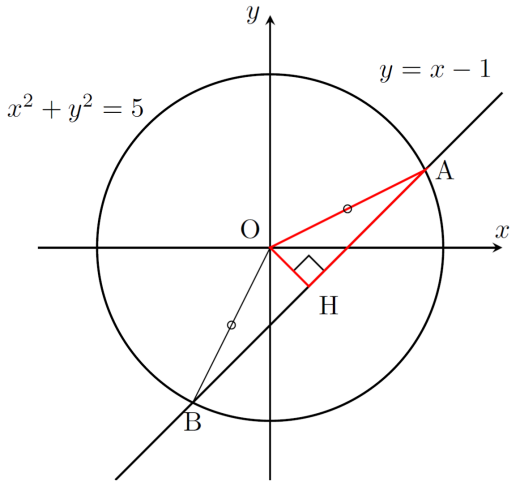
座標平面上に円 と直線 の交点を とおく。弦 の長さを求めよ。
まずは二等辺三角形は使わずに,素直に交点を計算する方法から見ていきましょう。
と の交点を求める。 の式に の式を代入すると, となり, が得られる。
こうして と の交点は となる。2点間の距離の公式を用いることで弦の長さは となる。
先ほどの別解のように二等辺三角形を用いて計算することもできます。円の中心と円周上の点を結ぶ線分の長さは半径の長さですね。半径は一定なので二等辺三角形が見つかるはずです。
円 の中心を とする。
, のどちらも半径である。円の式より半径は である。こうして で三角形 は二等辺三角形になる。
から弦 におろした垂線の足を とする。 は , の中点となる。
三平方の定理から次の式が得られる。
線分 の長さは,点 と直線 の距離である。 は と表される。点と直線の公式から である。こうして となる。
傾き・二等辺三角形・直角をうまく使って計算量を減らしましょう!











