【解答・解説】東大理系数学2019
※以下の解答と解説は東京大学が公表したものではなく,当サイトオリジナルのものです。問題は東京大学第2次試験問題からの引用です。
この記事では,東京大学の2019年度入学試験の理系数学について解説します。
文系はこちら
第一問 [積分]
第一問 [積分]
第二問 [図形の性質]
第二問 [図形の性質]
一辺の長さが の正方形 を考える。3点 ,, はそれぞれ辺 ,, 上にあり,3点 ,, および2点 ,, はどちらも面積が の三角形の3頂点であるとする。
の最大値,最小値を求めよ。
文系数学の第一問とほとんど同じです。
文系数学では初めから各点に座標が与えられており,計算を行うことで の最大値,最小値を計算しました。詳しくは 東大文系数学2019入試過去問解答解説 をご覧ください。
ここでは座標を取らない解法を紹介します。
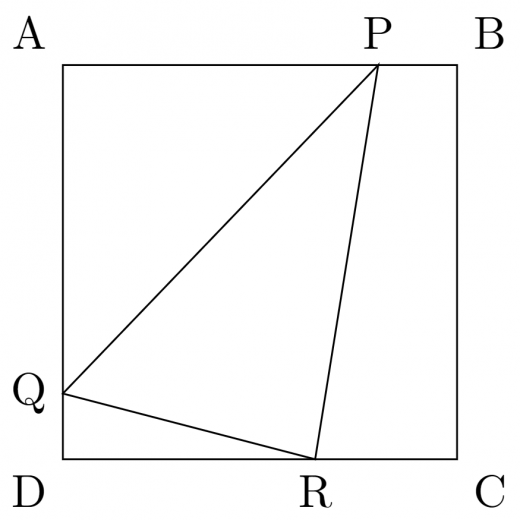
である。
条件より である。
また, であるため,
より であり, となる。 に代入して整理すると となる。
さらに両辺を で割ると を得る。
とおくと右辺は となる(以下これを とおく)。この三次関数の最大,最小を計算すればよい。
の範囲を調べる。すなわち の最大,最小を調べる。
は のとき,最大値 を取る。
より である。 の最大値は であるため,このとき は最小値 を取る。
よって であることが分かった。
より増減表は次のようになる。
よって最小値は ,最大値は となる。
第三問 [空間図形]
第三問 [空間図形]
座標空間内に5点 ,,,, を考える。線分 の中点 と線分 の中点 を通り,直線 に平行な平面を とする。さらに, は を満たす実数とし,点 を考える。
- 八面体 の平面 による切り口,および平面 の平面 による切り口を同一平面上に図示せよ。
- 八面体 の平面 により切り口が八角形となる の範囲を求めよ。
- 実数 が (2) で定まる範囲にあるとする。八面体 の平面 による切り口のうち , の部分を点 が動くとき,座標平面上で点 が動く範囲の面積を求めよ。
第三問は空間図形の問題でした。かなりの難問です。
八面体が歪んでいるため,図形をイメージすることが難しいです。立体をイメージすることが難しいときは,思い切って三次元的に考えるのをあきらめて,切断面などの二次元的な情報を考察しましょう。
平面 と平面 の交線を とおく。条件より と直線 は平行である。
直線 の式は であるため, の傾きは である。また,平面 は点 , を通るため,直線 は点 を通る。
こうして直線 の式は となる。
点 が平面 上にあるのは のとき,すなわち となるときである。
以上より によって場合分けをすると以下のようになる。
- のとき
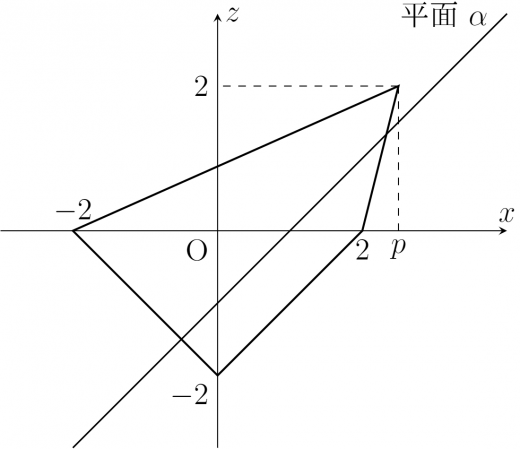
- のとき
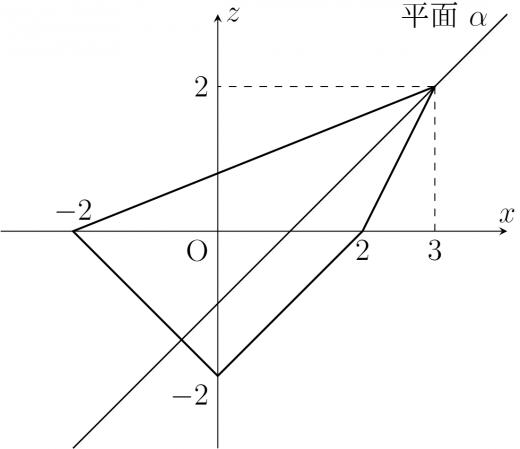
- のとき
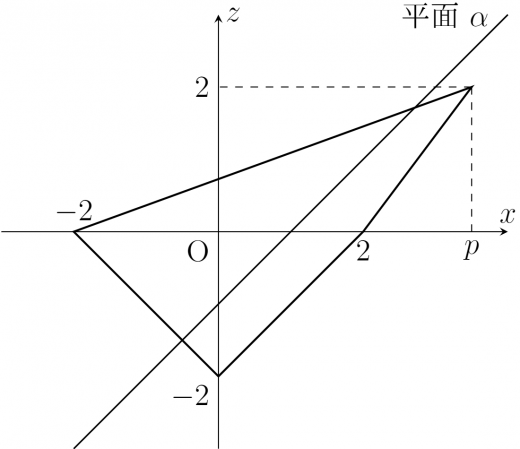
(1) を基に (2) を解きましょう。
によらず平面 は直線 ,直線 ,直線 ,直線 , と交わるため,少なくとも切り口は五角形以上になる。
- のとき
(1) より平面 は, と交わる。一方,,, とは交わらない。よって切り口は六角形である。
- のとき
(1) より平面 は,点 において ,,, と交わる。よって切り口は六角形である。
- のとき
(1) より平面 は,, と交わる。一方 , とは交わらない。よって切り口は八角形となる。
こうして答えは である。
具体的な座標を計算することになります。(1) で書いた 上の図を基に計算をします。
下図のように平面 と八面体の交点を ,,,,, とおく。これらを平面 に射影した点を順に , などとおく。
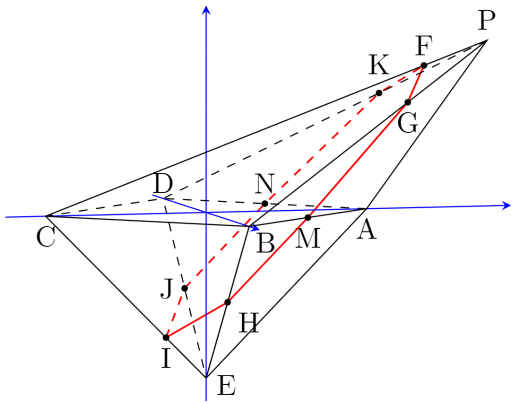
四角形 の面積を計算すればよい。
, の座標を計算する。
- の座標の計算
まず,平面 上での交点で考える。
直線 の傾きは であるので,式は となる。直線 と交点を計算すると となる。
よって, となる。
- の座標の計算
同じく 上で考える。
直線 の傾きは であるので,式は となる。直線 と交点を計算すると となる。
よって, となる。
以上より 平面上に射影すると下図のようになる。

よって面積は, となる。
当初は 平面に射影せずに面積を計算させる問題であったのかもしれません。この場合, 平面に射影した図形の面積(今回計算したもの)に, を掛ければ面積が得られます。
第四問 [整数]
第四問 [整数]
を 以上の整数とする。
-
と の最大公約数 を求めよ。
-
は整数の2乗にならないことを示せ。
第四問は整数の問題でした。文字が入っており戸惑うかもしれませんが,ユークリッドの互除法をイメージして解きましょう。
, とおく。
となるため, は の約数である。
-
が偶数のとき
は奇数であるため, である。 -
が奇数のとき
とおくと であるため, である。
(2) の結果を用いて (1) を解くことになります。
不等式評価と整数の離散性から が平方数にならないことを示します。応用できるテクニックなので覚えておきましょう。
後半では合同式を用います。合同式(mod)の意味とよく使う6つの性質 を復習しましょう。
が平方数となると仮定する。
- が偶数のとき
と は互いに素になるため,これらはどちらも平方数となる。
と は連続する2つの平方数である。 である。一方で である。よって は平方数とならない。
ゆえに は平方数にならない。
- が奇数のとき
である。
, とおく。
とおく。このとき である。
両辺を で割って を得る。
を法とする合同式を考えると となる。これは に反する。
こうして が奇数のときも は平方数にならない。
第五問 [極限]
第五問 [極限]
以下の問いに答えよ。
-
を 以上の整数とする。 についての方程式 は,ただ1つの実数解 をもつことを示せ。
-
(1) で定まる に対し, をもつことを示せ。
-
(1) で定まる数列 に対し, を求めよ。
第五問は極限の問題でした。
(1) では方程式の解がただ1つしか存在しないことを示します。
であることを用いると解が存在する範囲を絞り込むことができます。
中間値の定理もうまく活用しましょう。
-
のとき より に解はない。
-
のとき より に解はない。
-
のとき とおく。 となる。中間値の定理より は実数解を持つ。 となる。 のとき より である。よって はただ1つの実数解を持つ。
-
のとき より に解はない。
以上より はただ1つの実数解を持つ。
(2) は (1) より即座に分かります。
(1) より である。よって である。
(2) で示した不等式を頭におくと,はさみうちの原理が効きそうです。
の計算では をより扱いやすい形にすることがポイントです。 の計算から, が微分係数を計算する問題であることを気付けると Good です。
- の計算
(1),(2) の結果より である。
よって である。
より,はさみうちの原理から である。
- の計算
より である。よって となる。
- の計算
である。
より である。
第六問 [複素数]
第六問 [複素数]
複素数 および実数 が次の3条件を満たしながら動く。
- は相異なる。
- は4次方程式 の解である。
- 複素数 の実部は であり,虚部は でない。
- のうち,ちょうど2つが実数であり,残りの2つは互いに共役な複素数であることを示せ。
- を で表せ。
- 複素数 がとりうる範囲を複素数平面上に図示せよ。
第六問は複素数の問題でした。この問題も難問です。
が複素数解とすると, より, の共役も方程式の解となります。
ここから ,,, にアタリを付けることができます。
これに加えて3つ目の条件を上手く使うことが出来れば証明ができます。
が の解であったら, もまた の解である。
よって, は
- 共役な複素数のペア2つ
- 実数2つと共役な複素数のペア
- 実数4つ
のいずれか。
が全て実数のとき, は実数であるため,仮定に反する。
は共役な複素数のペア2つのときを考える。
-
, のとき
, より である。これは実数であるため,仮定に反する。 -
, のとき
より である。これは実数であるため,仮定に反する。
よって, は実数2つと共役な複素数のペアである。
複素数解は というようにおいたほうが共役複素数が扱いやすくなり,計算が簡単になります。
の場合, は実数であるため,条件に反する。
よって,, は実数, としてよい。
とおくと, となる。これは純虚数であるため, または とわかる。
- のとき
この場合において とおく。
解と係数の関係より である。これらを組み合わせると となる。こうして である。
- のとき
解と係数の関係より である。これらを組み合わせると , を得る。こうして である。
以上よりどちらの場合においても となる。
とおき条件式を計算しましょう。
とおく。
- のとき
, より である。
(2) より であった。これと合わせることで を得る。なお, は実数でないことから であったため, となる。
- のとき
より である。
(2) より , である。ここから を消去すると すなわち となる。
, で置き換えて を得る。なお, は実数でないことから であったため, となる。
以上より を図示すればよい。

東大理系数学2019入試過去問解説まとめ
東大理系数学2019入試過去問解説まとめ
第一問は冷静に処理しましょう。部分積分や置換積分をしっかり丁寧使えば計算できます。
第二問は文系数学との共通問題ですが,誘導が省かれているため難しく感じるかもしれません。
第三問は途中まで簡単なのでしっかり部分点を拾いたいです。
第四問は整数問題ですが,奇抜な発想が必要というわけではありません。ここも冷静に処理したいです。
第五問もできる限り解き切りたいです。最低限 , までは値を出したいところ。
第六問はかなりの難問です。最悪ここは捨てて他の問題に挑戦したほうがいいかもしれません。
全体的に解きにくいセットだったかもしれません。パッと見解けなくても落ち着いて地道に計算する根性が求められています。
第一問のうまい計算方法があったら教えてください。











