【解答・解説】東大文系数学2023

解と係数の関係より $\alpha + \beta = -1$，$\alpha \beta = -k$ である。

$$\begin{aligned} \alpha^2 + \beta^2 &= (\alpha + \beta)^2 - 2\alpha \beta\\ &= 1+2k\\ \alpha^3 + \beta^3 &= (\alpha + \beta)^3 - 3 \alpha \beta (\alpha + \beta)\\ &= -1 - 3 (-k) (-1)\\ &= -1-3k\\ \alpha^4 + \beta^4 &= (\alpha^2 + \beta^2)^2 - 2\alpha^2 \beta^2\\ &= (1+2k)^2 - 2k^2\\ &= 1 + 4k + 2k^2 \end{aligned}$$ であるため， $$\begin{aligned} \dfrac{\alpha^3}{1-\beta} + \dfrac{\beta^3}{1-\alpha} &= \dfrac{\alpha^3 (1-\alpha) + \beta^3 (1-\beta)}{(1-\alpha)(1-\beta)}\\ &= \dfrac{\alpha^3 + \beta^3 - \alpha^4 - \beta^4}{1 - (\alpha + \beta) + \alpha \beta}\\ &= \dfrac{-1-3k - (1+4k+2k^2)}{1 - (-1) - k}\\ &= \dfrac{2+7k+2k^2}{k-2}\\ &= 15 + 2(k-2) + \dfrac{24}{k-2} \end{aligned}$$ と計算される。

相加・相乗平均の不等式を用いると $$\begin{aligned} \dfrac{\alpha^3}{1-\beta} + \dfrac{\beta^3}{1-\alpha} &\geqq 15 + 2 \sqrt{2(k-2) \cdot \dfrac{24}{k-2}}\\ &= 15 + 8\sqrt{3} \end{aligned}$$ となる。等号が成立する $k$ が正の数であることを確認する。

等号は $2(k-2) = \dfrac{24}{k-2}$ のとき成立する。これを整理すると $(k-2)^2 = 12$，これを解くと $k = 2 \pm 2\sqrt{3}$ である。$k = 2+2\sqrt{3} > 0$ であるため，等号を満たす $k$ は存在する。

以上より最小値は $\mathbf{15+8\sqrt{3}}$ である。

点と直線の距離の公式から $$\begin{aligned} f(t) &= \dfrac{|2t - (3t^2-4t)|}{\sqrt{2^2 + 1^2}}\\ &= \dfrac{|6t-3t^2|}{\sqrt{5}}\\ &= \dfrac{3}{\sqrt{5}} |2t-t^2| \end{aligned}$$ である。絶対値を外すと $$f(t) = \begin{cases} \dfrac{3}{\sqrt{5}} (t^2 - 2t) &(-1 \leqq a \leqq 0)\\ \dfrac{3}{\sqrt{5}} (2t-t^2) &(0 \leqq a \leqq 2) \end{cases}$$ となる。

$-1 \leqq a \leqq 0$ のとき $$\begin{aligned} g(a) &= \int_{-1}^a \dfrac{3}{\sqrt{5}} (t^2 - 2t) dt\\ &= \dfrac{3}{\sqrt{5}} \Big[ \dfrac{1}{3} t^3 - t^2 \Big]_{-1}^{a}\\ &= \mathbf{\dfrac{1}{\sqrt{5}} (a^3 - 3a^2 + 4)} \end{aligned}$$

$0 \leqq a \leqq 2$ のとき $$\begin{aligned} &g(a)\\ &= \int_{-1}^0 \dfrac{3}{\sqrt{5}} (t^2 - 2t) dt + \int_{0}^a \dfrac{3}{\sqrt{5}} (- t^2 + 2t) dt\\ &= \Big[ \dfrac{1}{3} t^3 - t^2 \Big]_{-1}^{0} + \Big[ -\dfrac{1}{3} t^3 + t^2 \Big]_{0}^{a}\\ &= \mathbf{- \dfrac{1}{\sqrt{5}} (a^3 - 3a^2 - 4)} \end{aligned}$$

$h(a) = g(a) - f(a)$ とおく。 $$\begin{aligned} &h(a)\\ &= - \dfrac{1}{\sqrt{5}} (a^3 - 3a^2 - 4) - \dfrac{3}{\sqrt{5}} (2t-t^2)\\ &= - \dfrac{1}{\sqrt{5}} (a^3 - 6a^2 + 6a - 4) \end{aligned}$$ である。

$$\begin{aligned} h'(a) &= - \dfrac{1}{\sqrt{5}} (3a^2 - 12 a + 6)\\ &= - \dfrac{3}{\sqrt{5}} (a^2 - 4a+ 2) \end{aligned}$$ であるため。$h'(a) = 0$ を解くと $a = 2\pm \sqrt{2}$ となる。

$0\leqq a \leqq 2$ の範囲で増減表を書くと $$\begin{array}{c|ccccc} a & 0 & \cdots & 2-\sqrt{2} & \cdots & 2\\ \hline h'(a) && - & 0 & + &\\ \hline h(a) && \searrow & & \nearrow& \end{array}$$ となる。

$$\begin{aligned} h(0) &= \dfrac{4}{\sqrt{5}}\\ h(2) &= - \dfrac{1}{\sqrt{5}} (8-24+12-4)\\ &= \dfrac{8}{\sqrt{5}} \end{aligned}$$ である。

$$\begin{aligned} &a^3 -6a^2 + 6a - 4\\ &= (a - 2)(a^2 - 4a + 2) -4a \end{aligned}$$ より $$\begin{aligned} &h(2-\sqrt{2})\\ &= -\dfrac{\sqrt{2}}{\sqrt{5}} h'(2-\sqrt{2}) + \dfrac{4}{\sqrt{5}} (2-\sqrt{2})\\ &= 4\sqrt{2} \end{aligned}$$

以上より $h(a)$ は $a = 2$ で最大値 $\mathbf{\dfrac{8}{\sqrt{5}}}$，$a= 2-\sqrt{2}$ で最小値 $\mathbf{\dfrac{4}{\sqrt{5}} (2-\sqrt{2})}$ をとる。

12個の玉を並べる順列は $\dfrac{12!}{3! 4! 5!} = 27720$ 通りである。

黒玉と白玉を並べる順列は $\dfrac{8!}{3! 5!} = 56$ 通りである。

黒玉・白玉合わせて8個の玉の両端かその間に，赤玉4個を入れる組み合わせは ${}_9 \mathrm{C}_4 = 126$ 通りである。

よって求める確率は $$\dfrac{56 \cdot 126}{27720} = \mathbf{\dfrac{14}{55}}$$ となる。

黒玉も赤玉も隣り合わない確率を求めればよい。

(1) と同様に，まず黒玉と白玉を並べて，その後赤玉を並べることで組み合わせを計算する。

1. 黒玉と白玉を並べた時点で，黒玉は隣り合わないとき $$\text{例}: {}^{\vee} 白^{\vee} 黒^{\vee} 白^{\vee} 黒^{\vee} 白^{\vee} 白^{\vee} 白^{\vee} 黒^{\vee}$$ 白玉5個の両端かその間に，黒玉3個を隣り合わないように入れる組み合わせは ${}_6 \mathrm{C}_3 = 20$ 通りである。
   その上で赤玉を入れる組み合わせは，(1) 同様 $126$ 通りである。
   よって組み合わせは $20 \cdot 126$ 通りである。

2. 黒玉と白玉を並べた時点で，黒玉ちょうど2個が隣り合っているとき $$\text{例}: {}^{\vee} 白^{\vee} 白^{\vee} 黒^{\vee} 白^{\vee} 白^{\vee} 黒黒^{\vee} 白^{\vee}$$ 白玉5個の両端かその間に，黒玉1個と黒玉2個を隣り合わないように入れる組み合わせは $6 \cdot 5 = 30$ 通りである。
   その上で赤玉を入れる。1個は必ず黒玉2個の間に入れる。それ以外の4個は，8か所に入れることができるため，入れ方は ${}_8 \mathrm{C}_3 = 56$ 通りである。
   よって組み合わせは $30 \cdot 56$ 通りである。

3. 黒玉と白玉を並べた時点で，黒玉3個が隣り合っているとき $$\text{例}: {}^{\vee} 白^{\vee} 白^{\vee} 白^{\vee} 白^{\vee} 黒黒黒^{\vee} 白^{\vee}$$ 白玉5個の両端かその間に，黒玉3個を入れる組み合わせは $6$ 通りである。
   その上で赤玉を入れる。2個は必ず黒玉3個の間に入れる。それ以外の2個は，7か所に入れることができるため，入れ方は ${}_7 \mathrm{C}_2 = 21$ 通りである。
   よって組み合わせは $6 \cdot 21$ 通りである

以上をまとめると，組み合わせは $$20 \cdot 126 + 30 \cdot 56 + 6 \cdot 21 = 4326$$ 通りである。

よって黒玉も赤玉も隣り合わない確率は $\dfrac{4326}{27720}$ であるため，求めるべき条件付き確率は $$\begin{aligned} \dfrac{4326}{27720} \div \dfrac{56 \cdot 126}{27720} &= \dfrac{4326}{56 \cdot 126}\\ &= \mathbf{\dfrac{103}{168}} \end{aligned}$$ である。

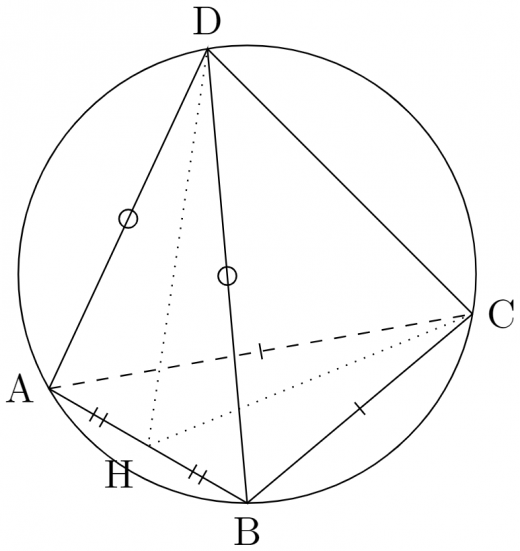
$\mathrm{C}$ から辺 $\mathrm{AB}$ に下した垂線の足を $\mathrm{H}$ とおく。

$$\dfrac{\mathrm{AH}}{\mathrm{CH}} = \tan \dfrac{1}{2} \angle \mathrm{ACB}$$ である。

$$\begin{aligned} \tan \dfrac{1}{2} \angle \mathrm{ACB} &= \sqrt{\dfrac{1 - \cos \angle \mathrm{ACB}}{1 + \cos \angle \mathrm{ACB}}}\\ &= \sqrt{\dfrac{1-\frac{4}{5}}{1+\frac{4}{5}}}\\ &= \dfrac{1}{3} \end{aligned}$$ である。こうして $\mathrm{CH} = \dfrac{3}{2}$ である。

よって面積は $$\dfrac{1}{2} \mathrm{AB} \cdot \mathrm{CH} = \mathbf{\dfrac{3}{4}}$$

問題文中の半径 $1$ の球の中心を $\mathrm{O}$ とおく。$\mathrm{D}$ から $\triangle \mathrm{ABC}$ に下した垂線の足を $\mathrm{I}$ とおく。

条件より $\triangle \mathrm{ABC}$ と $\triangle \mathrm{ABD}$ は合同である。ゆえに $\mathrm{CH} = \mathrm{DH} = \dfrac{3}{2}$ である。

また，条件より四面体 $\mathrm{ABCD}$ は平面 $\mathrm{CDH}$ に関して面対称な図形である。ゆえに $\mathrm{O}$，$\mathrm{I}$ は平面 $\mathrm{CDH}$ 上にある。

$\mathrm{A}$，$\mathrm{B}$ は球面上の点であるから $\mathrm{OA} = \mathrm{OB} = 1$ である。条件から $\mathrm{AB} = 1$ であったので，$\triangle \mathrm{OAB}$ は正三角形である。$\mathrm{H}$ は辺 $\mathrm{AB}$ の中点であったため，$\mathrm{OH} = \dfrac{\sqrt{3}}{2}$ である。

$\triangle \mathrm{OCH}$ について $\mathrm{OH} = \dfrac{\sqrt{3}}{2}$，$\mathrm{CH} = \dfrac{3}{2}$，$\mathrm{OC} = 1$ であるため，余弦定理から $$\begin{aligned} \cos \angle \mathrm{OHC} &= \dfrac{\mathrm{OH}^2 + \mathrm{CH}^2 - \mathrm{OC}^2}{2 \mathrm{OH} \cdot \mathrm{CH}}\\ &= \dfrac{\dfrac{3}{4} + \dfrac{9}{4} - 1}{2 \cdot \dfrac{\sqrt{3}}{2} \cdot \dfrac{3}{2}}\\ &= \dfrac{4}{3\sqrt{3}} \end{aligned}$$ である。また $$\sin \angle \mathrm{OHC} = \sqrt{1 - \left( \dfrac{4}{3\sqrt{3}}\right)^2} = \dfrac{\sqrt{11}}{3\sqrt{3}}$$

よって $$\begin{aligned} \sin \angle \mathrm{CHD} &= 2 \sin \angle \mathrm{OHC} \cos \angle \mathrm{OHC}\\ &= 2 \dfrac{\sqrt{11}}{3\sqrt{3}} \cdot \dfrac{4}{3\sqrt{3}}\\ &= \dfrac{8\sqrt{11}}{27} \end{aligned}$$ である。

こうして $$\begin{aligned} \mathrm{DI} &= \mathrm{DH} \sin \angle \mathrm{CHD}\\ &= \dfrac{3}{2} \dfrac{8\sqrt{11}}{27}\\ &= \dfrac{4\sqrt{11}}{9} \end{aligned}$$ となるため，体積は $$V = \dfrac{1}{3} \cdot \dfrac{3}{4} \cdot \dfrac{4\sqrt{11}}{9} = \mathbf{\dfrac{\sqrt{11}}{9}}$$ である。