ピックの定理
頂点がすべて格子点上にある多角形の面積は
内側の格子点数+辺上の格子点数
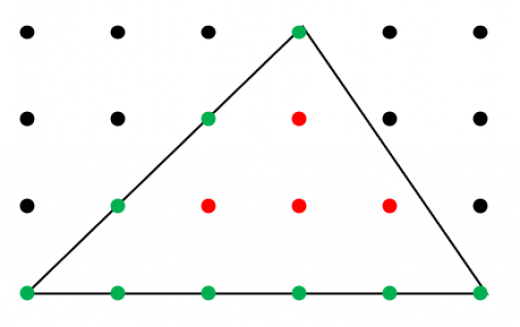
格子点とは, 座標も 座標も整数である点のことです。
上図の三角形において,
- 内側の格子点の数は 個
- 辺上の格子点の数(頂点も含める)は 個
ピックの定理より,面積は
ピックの定理の意味
ピックの定理の意味
-
格子点上にある多角形の面積をすばやく計算できる公式です、
-
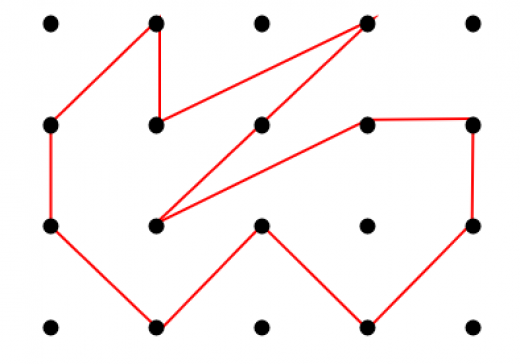
三角形の例だとそもそも簡単に面積を計算できますが,図のように複雑な多角形の場合は格子点の数を数えたほうが早いです。
-
「内側」は面積への寄与が で「辺上」は面積への寄与が というのは感覚と一致します。
応用
応用
面積を求める
ピックの定理は,面積を求めるのに使えます。
特に「直接面積を求めるのは難しいが,格子点の数は数えやすい」ような複雑な多角形の場合に活躍します。
格子点の数を求める
ピックの定理は,格子点の数を求めるのにも一応使えます。具体的には,「面積」と「辺上の格子点数」がわかれば「内側の格子点数」がわかります。
ただし,ピックの定理を使うと楽になる場面はあまりないです。あくまで検算に使えることもあるという程度です。
他の定理の証明
ピックの定理から以下の定理がわかります。
- すべての頂点が格子点である多角形の面積は の整数倍である。
- すべての頂点が格子点である正三角形は存在しない。
1はピックの定理から明らかです。2は1から導けます。
正三角形の辺の長さを とすると,面積は である。→正三角形の面積,正四面体の体積を求める公式
もし,すべての頂点が格子点である正三角形が存在したとすると,三平方の定理より は整数である。これは が無理数であることから1に矛盾。
ピックの定理の証明
ピックの定理の証明
きちんと書くとわりと大変です。
以下の順番で示す。やや難しいのは1だけ。
-
1辺 を共有する2つの図形 でピックの定理が成立するなら, と をくっつけた図形 でもピックの定理が成立する。

-
逆に, を と に分割し, と でピックの定理が成立するなら でもピックの定理が成立する(1を逆向きに見るとわかる)。
-
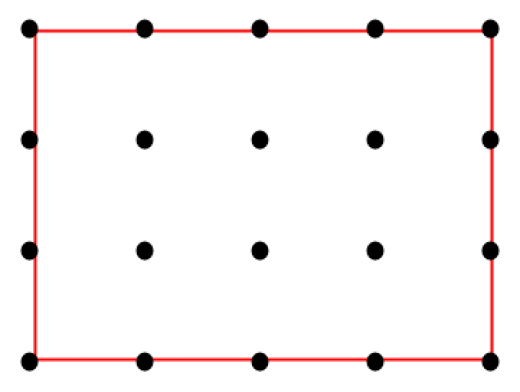
長方形についてピックの定理が成立する(簡単に確認できる)。
-
2本の座標軸と平行な辺を持つ直角三角形についてピックの定理が成立する(簡単に確認できる)。

-
任意の格子三角形についてピックの定理が成立する(大きい長方形から直角三角形を除くと,2と3と4からわかる)。

-
任意の格子多角形についてピックの定理が成立する(三角形分割すると1と5からわかる)。
他にも,オイラーの多面体定理を用いた証明や,コップに入れた水による説明もあります。
名前も主張も証明もおもしろいですが,実際の問題で活躍することは少ない印象です。











