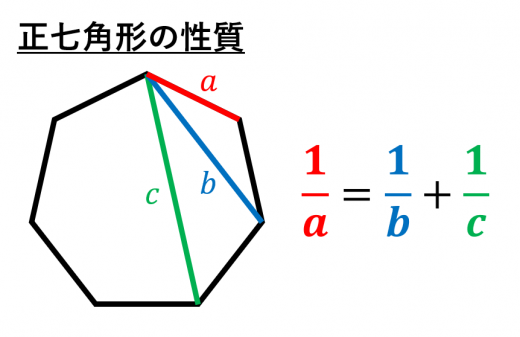
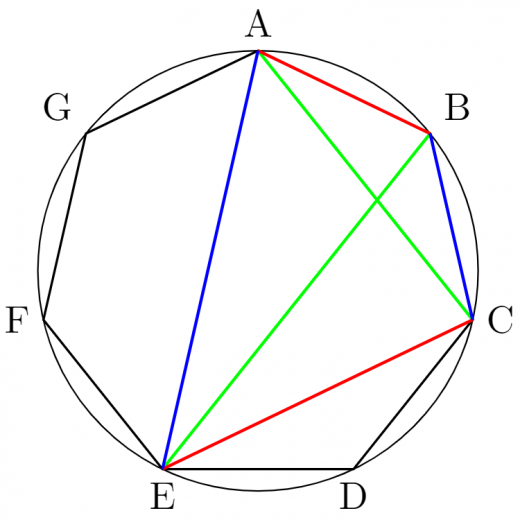
下図の正七角形 ABCDEFG を考えましょう。
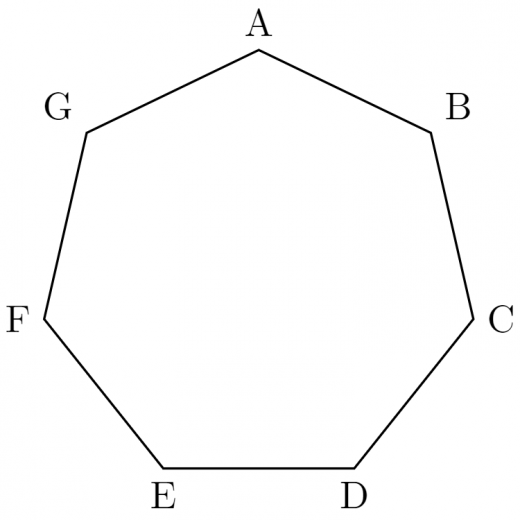
2つのステップに分けて計算をしていきます。
相似な二等辺三角形を作る
直線 BC と直線 DE の交点を H とおきます。
下図の青い三角形と赤い三角形は相似になります。
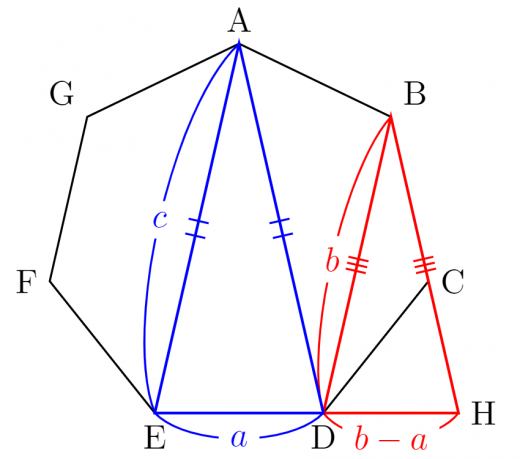
証明
正七角形の外接円を考える。弧 ED と弧 AB に対する円周角より ∠EAD=∠ADB となる。よって AE//BD
同様に AD//BC
以上より,2組の角がそれぞれ等しいので △AED と △BDH は相似になる。
相似比から計算する
相似比を見ると
AEDE=BDHD⋯(∗)
となります。
それぞれの辺の長さは,DE=a,AE=c,BD=b となります。
また,
DH=CH=BH−BC=BD−BC =b−a(△HCD は二等辺三角形)(△BDH は二等辺三角形)
と計算されます。
(∗) に代入して
ca=bb−a,つまり ca=1−ba を得ます。
両辺を a で割って
a1=b1+c1
が得られました。
今回紹介した等式の証明が灘高校や開成高校の入試問題として登場したこともあります。