相似比と面積比・体積比：いろいろな例と証明

更新日時 2022/06/21

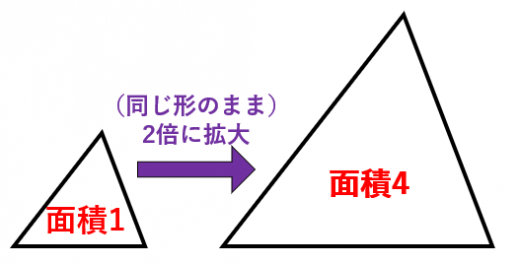
相似比と面積比

図形を $2$ 倍に拡大すると，面積は $4$ 倍になる。
図形を $k$ 倍に拡大すると，面積は $k\times k=k^2$ 倍になる。

相似な図形（形が同じで大きさが違う図形）について，相似比の意味と，面積比・体積比の公式について解説します。

相似・相似比
相似比と面積比
面積比が相似比の2乗になることの証明
応用例
相似な空間図形の体積比

相似・相似比まずは，相似と相似比について確認します。
相似とは，大雑把には同じ形（サイズは違っても良い）である図形のことです。例えば，図の2つの三角形は相似です。

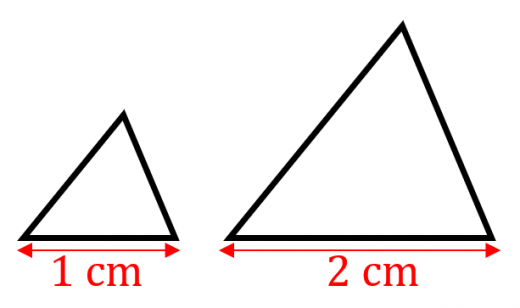（正確には，平行移動・回転・裏返し・拡大縮小でピッタリ重なる2つの図形のことを相似と言います）
相似比とは，拡大の倍率のことです。相似な図形の「対応する辺の長さの比が相似比」とも言えます。例えば，図の2つの三角形の相似比は 1:21:21:2 です。

相似比と面積比

相似比と面積比の関係

「面積比」は「相似比の2乗」と等しい

例1

2つの三角形が相似で相似比が $1:2$ のとき，面積比は， $1^2:2^2=1:4$ になる。相似な三角形

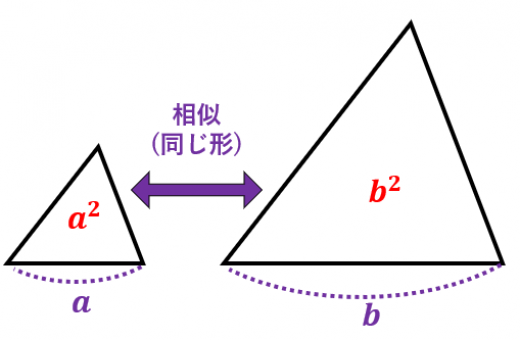
このように，相似比が $a:b$ なら面積比は $a^2:b^2$ になるというわけです。相似比と面積比

「図形を2倍に拡大すると，面積は4倍になる」と言うこともできます。簡単な図形（三角形・四角形）で例を見てみましょう。

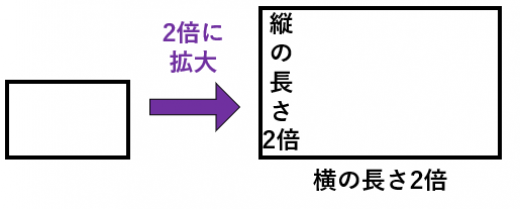
長方形の場合

例2. 長方形

長方形を $2$ 倍に拡大すると，縦の長さも横の長さも $2$ 倍になる。長方形の面積は「縦×横」なので，面積は $2\times 2=4$ 倍。長方形の場合の例

三角形の場合

例3. 三角形

三角形を $2$ 倍に拡大すると，底辺も高さも $2$ 倍になる。三角形の面積は底辺×高さ÷2なので，面積は $2\times 2=4$ 倍。

一般の図形の場合

長方形・三角形以外の図形の場合も，同様の事実が成り立知ます。

例4. その他の簡単な図形

円 $(S=\pi r^2)$ ，楕円 $(S=\pi ab)$ ，台形 $(S=\dfrac{h}{2}(a+b))$ など，平面図形の面積を表す公式は必ず長さの２次の項のみからなっており， $k$ 倍に拡大すると面積は $k^2$ 倍になることが分かります。

さらにより一般に，図形を $k$ 倍に拡大すると，面積は $k^2$ 倍になります。

面積比が相似比の2乗になることの証明

証明（大雑把な説明）

長方形や三角形の場合はさきほどの例で確認した。
四角形、五角形など多角形はいくつかの三角形に分割できる。図形を $k$ 倍に拡大すると，各三角形の面積は $k^2$ 倍になるので全体の面積も $k^2$ 倍になる。
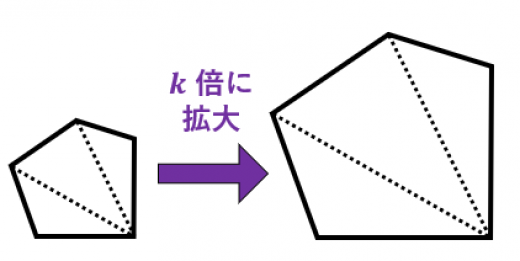
一般の図形は（無限に小さい）長方形に分割できる。図形を $k$ 倍に拡大すると，各長方形の面積は $k^2$ 倍になるので全体の面積も $k^2$ 倍になる。

上記2はわかりやすさのために記載しましたが，証明としては1と3だけで十分です。

応用例高校入試，大学入試で頻出の公式ですが，有名な定理の証明にも使われます。
錐体の体積公式に1/3がつくことの2通りの説明
ブラーマグプタの公式とその証明

相似な空間図形の体積比

次は空間図形の体積比です。いろいろな言い方がありますが，どれも同じ主張です。

相似比と体積比

図形を $2$ 倍に拡大すると，体積は $8$ 倍になる。
図形を $k$ 倍に拡大すると，体積は $k\times k\times k=k^3$ 倍になる。
相似な図形について，体積比＝相似比の3乗
相似比が $a:b$ なら体積比は $a^3:b^3$

体積比が相似比の3乗になることは，面積比と同じような説明で納得できます。

体積比が3乗になることの大雑把な説明

直方体の場合について正しい（体積は縦×横×高さなので $k$ 倍に拡大すると体積は $k^3$ 倍になる）
一般の空間図形は（無限に小さい）直方体の集まりとみなせる

この記事ではフラクタルなどのやばい図形は考えていません。

この記事の編集者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！