フーリエ級数展開の公式と意味

更新日時 2021/03/07

フーリエ級数展開

$f(x)$ が周期 $T$ の「まともな」関数なら

$f(x)=\dfrac{a_0}{2}+\displaystyle\sum_{n=1}^{\infty}\left(a_n\cos \dfrac{2\pi n x}{T}+b_n\sin \dfrac{2\pi nx}{T}\right)$

ただし，

$a_n=\dfrac{2}{T}\displaystyle\int_0^{T}f(x)\cos\dfrac{2\pi nx}{T}dx$

$b_n=\dfrac{2}{T}\displaystyle\int_0^{T}f(x)\sin\dfrac{2\pi nx}{T}dx$

フーリエ展開の意味，係数の導出，応用例として $\dfrac{\pi^2}{6}$ に収束する有名な級数の話を解説します。

フーリエ級数展開とは
フーリエ級数展開の条件
フーリエ係数の導出
具体例

フーリエ級数展開とは〜やりたいこと〜
与えられた周期
TTT
 の関数を，周期
TTT
（の約数もOK）の三角関数（サインとコサイン）の和で表現したいという話です。
〜なぜ 2πnxT\dfrac{2\pi nx}{T}T2πnx​ が登場するのか〜
g(x)=sin⁡2πnxTg(x)=\sin \frac{2\pi nx}{T}g(x)=sinT2πnx​
 の周期は
Tn\frac{T}{n}nT​
 であり，g(x+T)=g(x)g(x+T)=g(x)g(x+T)=g(x)
 を満たします。
h(x)=cos⁡2πnxTh(x)=\cos \frac{2\pi nx}{T}h(x)=cosT2πnx​
 も同様です。そこで，これらの「
TTT
 ズラしてもとに戻る単純な関数の無限和」で「
TTT
 ズラしてもとに戻る関数
f(x)f(x)f(x)
」を表現します。
特に，f(x)f(x)f(x)
 の周期が
2π2\pi2π
 の場合，使う三角関数は
sin⁡nx,cos⁡nx\sin nx,\cos nxsinnx,cosnx
 とシンプルな形になります。

フーリエ級数展開の条件冒頭では「まともな」関数と述べてぼかしました。やばい関数だとフーリエ級数展開できませんが，
応用上登場する関数はだいたいフーリエ級数展開できるのでそんなに気にしなくてOKです。
例えば
f(x)f(x)f(x)
 が連続かつ導関数も連続なら問題なしです。
f(x)f(x)f(x)
 や
f′(x)f'(x)f′(x)
 に不連続点がちょいちょいあっても問題なし（不連続点以外で各点収束）です。
フーリエ級数展開できるための詳しい条件については専門書を参照して下さい。

フーリエ係数の導出フーリエ係数
an, bna_n,\:b_nan​,bn​
 の形がなぜ冒頭の式で表されるのか説明します。三角関数の積分にある程度慣れている必要があります。
（係数の導出）
〜 a0a_0a0​ について〜
f(x)=a02+∑n=1∞(ancos⁡2πnxT+bnsin⁡2πnxT)f(x)=\dfrac{a_0}{2}+\displaystyle\sum_{n=1}^{\infty}\left(a_n\cos \dfrac{2\pi n x}{T}+b_n\sin \dfrac{2\pi nx}{T}\right)f(x)=2a0​​+n=1∑∞​(an​cosT2πnx​+bn​sinT2πnx​)
の両辺を
000
 から
TTT
 まで積分すると（右辺の周期関数の積分が全て
000
 になるので），∫0Tf(x)dx=a02T\displaystyle\int_0^{T}f(x)dx=\dfrac{a_0}{2}T∫0T​f(x)dx=2a0​​T
つまり，a0=2T∫0Tf(x)dxa_0=\dfrac{2}{T}\displaystyle\int_0^Tf(x)dxa0​=T2​∫0T​f(x)dx
〜 ana_nan​（n≥1n\geq 1n≥1）について〜
f(x)=a02+∑n=1∞(ancos⁡2πnxT+bnsin⁡2πnxT)f(x)=\dfrac{a_0}{2}+\displaystyle\sum_{n=1}^{\infty}\left(a_n\cos \dfrac{2\pi n x}{T}+b_n\sin \dfrac{2\pi nx}{T}\right)f(x)=2a0​​+n=1∑∞​(an​cosT2πnx​+bn​sinT2πnx​)
の両辺に
cos⁡2πnxT\cos\dfrac{2\pi nx}{T}cosT2πnx​
 をかけて
000
 から
TTT
 まで積分すると，∫0Tf(x)cos⁡2πnxTdx=an2T\displaystyle\int_0^Tf(x)\cos\dfrac{2\pi nx}{T}dx=\dfrac{a_n}{2}T∫0T​f(x)cosT2πnx​dx=2an​​T
（→注1）
より
an=2T∫0Tf(x)cos⁡2πnxTdxa_n=\dfrac{2}{T}\displaystyle\int_0^{T}f(x)\cos\dfrac{2\pi nx}{T}dxan​=T2​∫0T​f(x)cosT2πnx​dx
〜 bnb_nbn​ について〜
同じように両辺に
sin⁡2πnxT\sin\dfrac{2\pi nx}{T}sinT2πnx​
 をかけて
000
 から
TTT
 まで積分するとOK。
注1：三角関数の直交性という積分公式を用いています。→三角関数の積の積分と直交性
この公式により右辺の各項の積分はほとんど
000
 になり，∫0Tancos⁡22πnxTdx=an2T\displaystyle\int_0^Ta_n\cos^2\dfrac{2\pi nx}{T}dx=\dfrac{a_n}{2}T∫0T​an​cos2T2πnx​dx=2an​​T
 だけが生き残ります。
注2：なお，積分と無限和の順序交換が可能であることを仮定しています。この部分が厳密ではありませんが，フーリエ係数の形の意味を見るには十分でしょう。
なお，フーリエ展開には複素指数関数を用いた表現もあります。→複素数型のフーリエ級数展開とその導出

具体例

例題

$y=x^2\:(-\pi\leq x \leq \pi)$ を周期 $2\pi$ の関数になるように拡張した関数 $f(x)$ のフーリエ級数展開を求めよ。

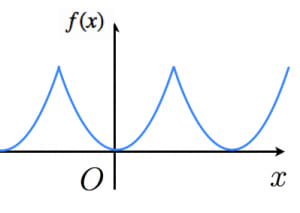
フーリエ展開の例

解答

フーリエ係数を求める。周期性に注意すると $0$ から $2\pi$ までの積分値は $-\pi$ から $\pi$ までの積分値と等しいことが分かる。

$a_0=\dfrac{2}{2\pi}\displaystyle\int_{-\pi}^{\pi}x^2dx=\dfrac{2}{3}\pi^2$

$a_n=\dfrac{2}{2\pi}\displaystyle\int_{-\pi}^{\pi}x^2\cos nxdx$ ，瞬間部分積分を用いて計算すると $a_n=(-1)^n\dfrac{4}{n^2}$

$b_n=\dfrac{2}{2\pi}\displaystyle\int_{-\pi}^{\pi}x^2\sin nxdx$ であり，被積分関数は奇関数なので $b_n=0$

つまり， $f(x)=\dfrac{\pi^2}{3}+\displaystyle\sum_{n=1}^{\infty}(-1)^n\dfrac{4}{n^2}\cos nx$

ちなみにこの式に $x=\pi$ を代入すると $\pi^2=\dfrac{\pi^2}{3}+4\displaystyle\sum_{n=1}^{\infty}\dfrac{1}{n^2}$

となり，有名な級数 $\displaystyle\sum_{n=1}^{\infty}\dfrac{1}{n^2}=\dfrac{\pi^2}{6}$ を得ます。→バーゼル問題の初等的な証明

フーリエ展開を使えば他にもいろいろな級数が導出できます！

この記事の編集者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！