デルタマトロイド

更新 2021/03/07

以前，マトロイドというものについて紹介しました。→マトロイドの定義と具体例

この記事では，マトロイドの一般化であるデルタマトロイドについて紹介します。

デルタマトロイドの定義

有限集合 $E$ とその部分集合族 $\mathcal{F}$ について，以下の2つの条件が成立するとき $(E,\mathcal{F})$ のペアをデルタマトロイドと言う。

$\mathcal{F}$ は空でない。
任意の $X,Y\in \mathcal{F}$ と任意の $i\in X\mathbin{\Delta}Y$ に対して，ある $j\in X\mathbin{\Delta}Y$ が存在して， $X\mathbin{\Delta}\{i,j\}\in\mathcal{F}$

対称差

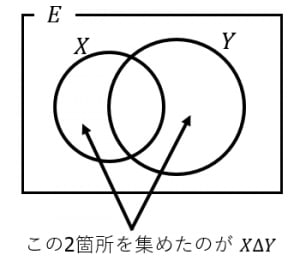
ただし，2つの集合 $X,Y$ に対して $X\mathbin{\Delta}Y$ は対称差（どちらか片方のみに属する要素を集めた集合）を表します。→集合の記号の意味まとめ

上記の定義には大文字のデルタ「 $\Delta$ 」が3つも登場しています。

デルタマトロイドはマトロイドの一般化になっています。つまり，任意のマトロイド（独立集合族ではなく基族で考える）は，特殊な（ $\mathcal{F}$ に属する集合の要素数が全て等しい）デルタマトロイドです。

デルタマトロイドの例

デルタマトロイドなんて使う機会あるのか？ と思うかもしれませんが，実は意外と身近な存在かもしれません。
定理
EEE：（枝を1本以上持つ）無向グラフの頂点集合。
F\mathcal{F}F：マッチングの端点集合を集めたもの。
とすると，(E,F)(E,\mathcal{F})(E,F)
 はデルタマトロイド。
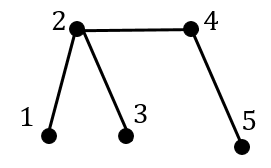
例えば，図のようなグラフについては，
E={1,2,3,4,5}E=\{1,2,3,4,5\}E={1,2,3,4,5}
F={∅,{1,2},{2,3},{2,4},{4,5}{1,2,4,5},{2,3,4,5}}\mathcal{F}=\{\emptyset,\{1,2\},\{2,3\},\{2,4\},\{4,5\}\\
\{1,2,4,5\},\{2,3,4,5\}\}F={∅,{1,2},{2,3},{2,4},{4,5}{1,2,4,5},{2,3,4,5}}
となります。
{{1,2},{4,5}}\{\{1,2\},\{4,5\}\}{{1,2},{4,5}}
 はマッチングなので，{1,2,4,5}\{1,2,4,5\}{1,2,4,5}
 が
F\mathcal{F}F
 に属している，という感じです。
→二部グラフの最大マッチングと増加道

上記の定理の証明

証明

デルタマトロイドの定義の2を確認すればよい。そこで，

$X,Y\in\mathcal{F}$ と $i\in X\mathbin{\Delta}Y$ が与えられた状況を考える。

$\mathcal{F}$ の定義より， $X$ を端点集合とするマッチング $M_X$ と $Y$ を端点集合とするマッチング $M_Y$ をとってこれる。

$i$ に対応する頂点は $M_X$ と $M_Y$ の片方にのみ属するので「交互路」の端点である。

デルタマトロイドとマッチング

そこで，この交互路のもう片方の端点に対応する要素を $j$ とすると， $X\mathbin{\Delta}\{i,j\}$ も，とあるマッチングの端点集合になっていることが分かる（交互路の端が $M_X$ の枝なのか $M_Y$ の枝なのかによって4パターンあるが，それぞれ赤を青に「切り替える」ことで $X\mathbin{\Delta}\{i,j\}$ を端点集合とするマッチングを構成できる）。

つまり， $X\mathbin{\Delta}\{i,j\}\in\mathcal{F}$

デルタマトロイドが好きな友人にそそのかされて，マニアックな記事を書いてしまいました。

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！