傘型分割(傘型積分)と斜回転体の体積
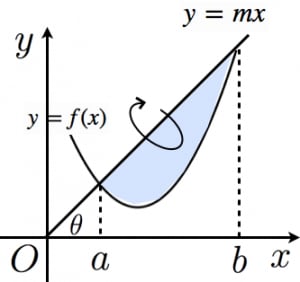
図のように,直線 と曲線 で囲まれた部分を の回りに回転させてできる図形の体積は, ただし, は と 軸のなす角で,
傘型分割の考え方を使って斜回転体の体積を求めてみましょう。
傘型分割の具体例
傘型分割の具体例
まずは傘型分割を使う具体例です。
と で囲まれた図形を の回りに回転させてできる図形の体積 を求めよ。
2つの曲線の交点は と であり, とした傘型分割公式により, は
- 計算がけっこう大変です。
- この例題のように のまわりに回転させる場合が頻出です。
- 追記:読者の方からベータ関数の積分公式を用いれば上記の計算は簡単にできるとご指摘いただきました:
積分の部分
傘型分割の諸注意
傘型分割の諸注意
- 回転体の体積を求めさせる問題の多くは回転軸が 軸または 軸です。しかし,たまに回転軸が斜めになっているものも出題されます。そのような斜回転体の求積に対応するための公式が傘型分割公式です。
- 公式を丸ごと覚える必要はありません(覚えてもよいですが)。慣れれば導出は一瞬でできます。
傘型分割の簡単な説明
傘型分割の簡単な説明
厳密な証明は他の求積公式と同様にはさみ打ちの原理を使う必要があります(参照:→なぜ定積分で面積が求まるのか)。
以下は「簡単な説明」です。
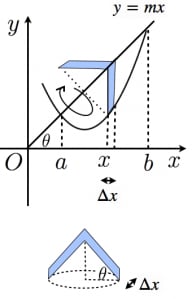
まず,回転させる前の図形を縦に細かく切る。
から の間の部分を回転させると傘の帽子の部分のような形の図形になる。 が十分小さいとき,この図形の体積は「円錐の側面積 厚さ 」で近似できる。
この円錐は,母線の長さが で半径が なので,側面積は となる。よって,これに をかけると微小な傘の体積が得られ, から まで積分して公式を得る。
傘型分割の応用
傘型分割の応用

傘型分割は発展的な話題であり,計算もそこそこ大変なので,出題されるほとんどの問題は基本的な形です。しかし,以下のように一捻りある問題に対しても傘型分割は使えます。
- 回転させる前の図形が回転軸と離れている場合(青い図形):
これは,「全体(青+緑)ー上側の部分(緑)」とみなしてそれぞれに傘型分割公式を使えばOKです。 - 回転させる前の図形が回転軸とかぶっている場合(赤い図形):
これは回転軸が斜めでない場合にも頻出ですが,回転軸に関して折り返して片側に集めてから傘型分割公式を使えばOKです。
図を書くのに苦労しました。不器用な図ですみませんm(__)m











