定積分
高校数学で習う定積分について基礎からわかりやすく説明します。
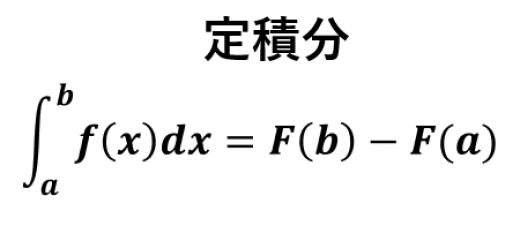
定積分とは
定積分とは
とは, のことを表す。
ただし, は微分すると になる関数。
のことを の区間 における定積分と言います。
を計算せよ。
微分すると になる関数として が取れる。
よって,
※ 微分すると になる関数として などと定数を足したものも取れますが, の計算結果は必ず で同じになります。
定積分 を計算せよ。
とすれば
よって定積分の値は
定積分の計算方法
定積分の計算方法
例題1で見たように,定積分 の計算は以下の2ステップでできます。
- 微分すると になる関数 を求める
- に と を代入して引き算する
2はただ計算するだけです。
1は不定積分の計算です。つまり,定積分を計算するためにも,不定積分をしっかりマスターすることが大事と言えます。
→不定積分の意味・公式・例題
定積分 を計算せよ。
-
微分して になる関数を計算する。つまり の不定積分を計算すると,
-
より,求める定積分の値は
※ステップ1の不定積分の計算は不定積分の意味・公式・例題の例題3で詳しく解説しています。
補足:定積分の表記方法
定積分の計算の途中で出てくる のことを と書くことがあります。この表記を使うと,例題2の解答は以下のようにかけます:
補足:定積分は計算が大変
定積分のステップ2はただ計算するだけですが,計算量が多くミスしやすいです。そのため,工夫して計算量を減らすことも大事です。
例えば,偶関数や奇関数の場合に使えるテクニック→偶関数と奇関数の意味,性質などまとめや,1/6公式 を知っておくとよいです。
定積分の応用:なぜ定積分を学ぶのか
定積分の応用:なぜ定積分を学ぶのか
定積分はなぜ という定義なのか? 何の役に立つのか?
→ いろいろな応用があるから。例えば,定積分を使うと面積・体積・曲線の長さなど図形に関するいろいろな量が計算できます。
-
図形の面積:
例えば,以下の斜線部分の面積は という定積分で計算できます。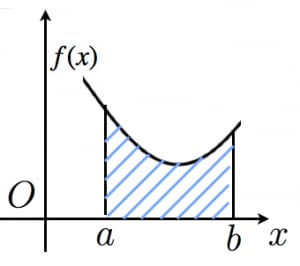 →なぜ定積分で面積が求まるのか
→なぜ定積分で面積が求まるのか -
図形の体積:
例えば,錐体の体積や球の体積公式を導出するのに定積分が活躍します。
→錐体の体積に1/3がつくことの2通りの説明 -
曲線の長さ:
曲線の長さの計算でも定積分が活躍します。
→曲線の長さを計算する積分公式(弧長積分)
定積分と不定積分
定積分と不定積分
定積分と不定積分の違い・関係を整理します。
定積分と不定積分の違い
-
定積分は のように の上下に数がくっつきます。不定積分は のように の上下に数はくっつきません。
-
定積分の計算結果は数です。不定積分の計算結果は関数(の集合)です。
定積分と不定積分の関係
-
不定積分の結果に区間の両端の値を代入すれば 定積分が計算できます。つまり,不定積分が計算できれば定積分も計算できます。
-
しかし「不定積分が計算できなくても定積分なら計算できる場合」もあります。
微分→不定積分→定積分 の順に1つずつしっかり理解していくことが重要です。不定積分はモチベーションを維持しにくいですが,定積分までたどりつけば面積などいろいろな計算ができて楽しいです。











