定理2
ドーナツの表面積は,4π2rR
表面積も2通りの計算方法を紹介します。まずは,体積の結果(定理1)を使った方法です。
証明1(大雑把だがおもしろい)
R を固定して,体積と表面積を r の関数とみなす。それぞれ V(r),S(r) とおく。
すると,Δr が十分小さいとき,
V(r)+S(r)Δr≒V(r+Δr)
となる(→補足)。変形すると,
ΔrV(r+Δr)−V(r)≒S(r)
Δr→0 の極限を考えると,drdV(r)=S(r)
よって,定理1の結果 V(r)=2π2r2R を r で微分すると S(r)=4π2rR
補足:「小さいドーナツ」に「ドーナツの表面積×追加した厚み」を加えると「大きいドーナツ」になります。
なお,「体積の微分が表面積」という関係は,球についても成立します。→球の体積と表面積の公式の覚え方・積分での求め方内の「球の表面積の求め方2」参照。
次は,表面積を計算する公式 S=∫x0x12πy1+y′2dx を使った計算方法です。この公式を知らない方は楕円体・回転楕円体の意味と体積・表面積の定理3の証明を読んでみてください。
証明2
体積の場合と同じく,円の式を
y1=R+r2−x2,y2=R−r2−x2 とおく。
 表面積は,
表面積は,
∫−rr2πy11+y1′2dx+∫−rr2πy21+y2′2dx
となる。ここで,
y1′=(−x)r2−x21
1+y1′2=1+r2−x2x2=r2−x2r2
となり,1+y2′2 も同じ式になる。よって,表面積は
∫−rr2π×2R×r2−x2rdx
ここで,x=rcosθ と置換すると,上式は
4πR∫π0sinθ−rsinθdθ=4π2rR
パップスギュルダンの定理が活躍する代表的な例です!
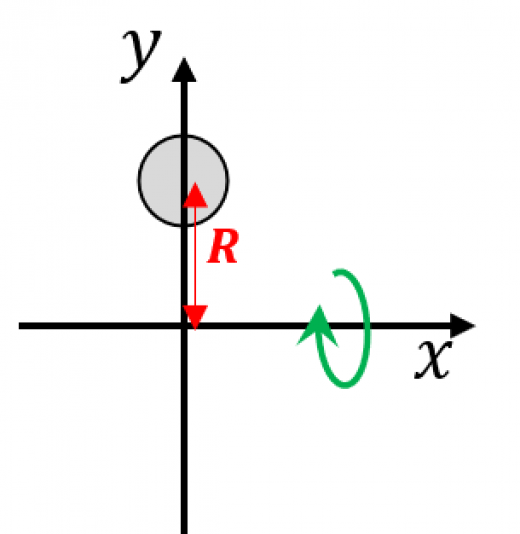
 半径 の円を軸のまわりに回転させてできる図形を考える。軸から円の中心までの距離を とする。
半径 の円を軸のまわりに回転させてできる図形を考える。軸から円の中心までの距離を とする。
 表面積は,
表面積は,










