パップスギュルダンの定理とその証明

更新 2021/12/15

パップスギュルダンの定理

面積が $S$ である平面図形 $A$ がある。 $A$ を直線 $l$ の回りに回転させてできる回転体の体積 $V$ は，

$V=2\pi g_xS=$ (重心の移動距離) $\times S$

（ $g_x$ は重心と回転軸の距離）

ただし， $A$ を回転させる過程で $A$ 自身とは重ならないとする。

パップスギュルダンの定理という面白い定理を紹介します。

パップスギュルダンの定理に関して

定理の主張に登場する「重心」については後で詳しく解説します。
「重心の移動距離」×「面積」で体積が求まるというのはかなり綺麗で覚えやすいです。
パップスギュルダンの定理は，検算テクニック＆雑学として知っておくとよいです。ただし，残念ながら，パップスギュルダンの定理一発で答えが求まるような入試問題は，少なくとも私は見たことがありません。
パップスギュルダンの定理を使うには「回転で自分自身と重ならない」という条件が必要です。例えば図において上側の図形には使えますが，下側の図形には使えません。

重心とは

パップスギュルダンの定理を使うには，図形
AAA
の重心を求める必要があります。重心というのは，感覚的には質量中心，つまり「図形
AAA
を指一本の上に載せたときにバランスをとれる点」です。
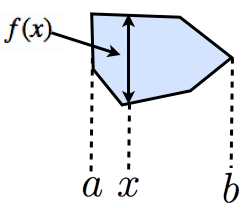
厳密には，重心の
xxx
座標は以下のように積分を使って定義されます：
gx=∫abxf(x)dx∫abf(x)dx=∫abxf(x)dxS  g_x=\dfrac{\int_a^b xf(x)dx}{\int_a^b f(x)dx}=\dfrac{\int_a^b xf(x)dx}{S}\:\:gx​=∫ab​f(x)dx∫ab​xf(x)dx​=S∫ab​xf(x)dx​

ただし，f(x)f(x)f(x)
は
xxx
の点での図形の「長さ」です。
重心の
xxx
座標は，
図形の xxx 座標がどのへんに分布しているか，その「期待値」のようなものです。yyy
座標についても同様です。
三角形に関しては高校数学で習う「いつもの重心（中線の交点）」と同じになります。また，円や長方形など対称性の高い図形では，積分を行わなくても重心の位置が分かります。

パップスギュルダンの定理の証明

バームクーヘン積分の例と証明を用いればパップスギュルダンの定理が一発で証明できます！

証明

バウムクーヘン分割の公式より，

$V=2\pi\displaystyle\int_a^b xf(x)dx$

ここで，重心の定義式より， $g_xS=\displaystyle\int_a^b xf(x)dx$ なので

$V=2\pi g_xS$ となる。

この証明からも分かる通り，パップスギュルダンの定理はバウムクーヘン分割を，重心を使って言い換えたものに過ぎません。

パップスギュルダンの定理の応用

ドーナツの体積を計算できます！→ドーナツ（トーラス体・円環体）の体積・表面積を2通りの方法で計算
パップスギュルダンの定理を逆に使えば，重心の座標を求めることもできます。

例

半径 $r$ の半円の重心の位置を求める。

パップスギュルダンの応用

上下対称な図形なので中心からの距離 $g_x$ のみを求めればよい。

回転させると球になるので， $V=\dfrac{4}{3}\pi r^3$

また， $S=\dfrac{1}{2}\pi r^2$

よって，パップスギュルダンの定理より，

$\dfrac{4}{3}\pi r^3=2\pi g_x\cdot\dfrac{1}{2}\pi r^2$

よって， $g_x=\dfrac{4r}{3\pi}$

→高校数学の問題集　～最短で得点力を上げるために～のT106では，パップスギュルダンの定理が活躍する例題と，その問題の3通りの解答を紹介しています。

ギュルっと回してdone

Tag:積分を用いた面積，体積の求積公式まとめ

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！